题目内容
7．已知△ABC是边长为2的等边三角形，P为平面ABC内一点，则$\overrightarrow{PA}$•（$\overrightarrow{PB}$+$\overrightarrow{PC}$）的最小值是（ ）| A． | -2 | B． | -$\frac{3}{2}$ | C． | -$\frac{4}{3}$ | D． | -1 |
分析 根据条件建立坐标系，求出点的坐标，利用坐标法结合向量数量积的公式进行计算即可．
解答 解：建立如图所示的坐标系，以BC中点为坐标原点，
则A（0，$\sqrt{3}$），B（-1，0），C（1，0），
设P（x，y），则$\overrightarrow{PA}$=（-x，$\sqrt{3}$-y），$\overrightarrow{PB}$=（-1-x，-y），$\overrightarrow{PC}$=（1-x，-y），
则$\overrightarrow{PA}$•（$\overrightarrow{PB}$+$\overrightarrow{PC}$）=2x2-2$\sqrt{3}$y+2y2=2[x2+（y-$\frac{\sqrt{3}}{2}$）2-$\frac{3}{4}$]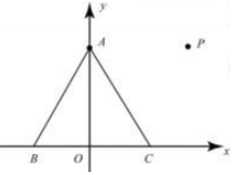
∴当x=0，y=$\frac{\sqrt{3}}{2}$时，取得最小值2×（-$\frac{3}{4}$）=-$\frac{3}{2}$，
故选：B
点评 本题主要考查平面向量数量积的应用，根据条件建立坐标系，利用坐标法是解决本题的关键．
练习册系列答案
相关题目
如图，正方体ABCD-A1B1C1D1的棱长为a，在此几何体中，给出下面四个结论：①异面直线A1D与AB1所成角为60°；②直线A1D与BC1垂直；③直线A1D与BD1平行；④三棱锥A-A1CD的体积为$\frac{1}{6}{a^3}$，其中正确的结论个数是（ ）
15．为了监控某种零件的一条生产线的生产过程，检验员每隔30min从该生产线上随机抽取一个零件，并测量其尺寸（单位：cm）．下面是检验员在一天内依次抽取的16个零件的尺寸：
经计算得 $\overline{x}$=$\frac{1}{16}$$\sum_{i=1}^{16}$xi=9.97，s=$\sqrt{\frac{1}{16}\sum_{i=1}^{16}（{x}_{i}-\overline{x}）^{2}}$=$\sqrt{\frac{1}{16}（\sum_{i=1}^{16}{{x}_{i}}^{2}-16{\overline{x}}^{2}）$≈0.212，$\sqrt{\sum_{i=1}^{16}（i-8.5）^{2}}$≈18.439，$\sum_{i=1}^{16}$（xi-$\overline{x}$）（i-8.5）=-2.78，其中xi为抽取的第i个零件的尺寸，i=1，2，…，16．
（1）求（xi，i）（i=1，2，…，16）的相关系数r，并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小（若|r|＜0.25，则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小）．
（2）一天内抽检零件中，如果出现了尺寸在（$\overline{x}$-3s，$\overline{x}$+3s）之外的零件，就认为这条生产线在这一天的生产过程可能出现了异常情况，需对当天的生产过程进行检查．
（ⅰ）从这一天抽检的结果看，是否需对当天的生产过程进行检查？
（ⅱ）在（$\overline{x}$-3s，$\overline{x}$+3s）之外的数据称为离群值，试剔除离群值，估计这条生产线当天生产的零件尺寸的均值与标准差．（精确到0.01）
附：样本（xi，yi）（i=1，2，…，n）的相关系数r=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sqrt{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}\sqrt{\sum_{i=1}^{n}（{y}_{i}-\overline{y}）^{2}}}$，$\sqrt{0.008}$≈0.09．
| 抽取次序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 零件尺寸 | 9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
| 抽取次序 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 零件尺寸 | 10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
（1）求（xi，i）（i=1，2，…，16）的相关系数r，并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小（若|r|＜0.25，则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小）．
（2）一天内抽检零件中，如果出现了尺寸在（$\overline{x}$-3s，$\overline{x}$+3s）之外的零件，就认为这条生产线在这一天的生产过程可能出现了异常情况，需对当天的生产过程进行检查．
（ⅰ）从这一天抽检的结果看，是否需对当天的生产过程进行检查？
（ⅱ）在（$\overline{x}$-3s，$\overline{x}$+3s）之外的数据称为离群值，试剔除离群值，估计这条生产线当天生产的零件尺寸的均值与标准差．（精确到0.01）
附：样本（xi，yi）（i=1，2，…，n）的相关系数r=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sqrt{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}\sqrt{\sum_{i=1}^{n}（{y}_{i}-\overline{y}）^{2}}}$，$\sqrt{0.008}$≈0.09．
2．（1+$\frac{1}{x^2}$）（1+x）6展开式中x2的系数为（ ）
| A． | 15 | B． | 20 | C． | 30 | D． | 35 |
12．已知x，y满足约束条件$\left\{\begin{array}{l}{x-y+3≤0}\\{3x+y+5≤0}\\{x+3≥0}\end{array}\right.$，则z=x+2y的最大值是（ ）
| A． | 0 | B． | 2 | C． | 5 | D． | 6 |
16．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}-x+3，x≤1}\\{x+\frac{2}{x}，x＞1}\end{array}$，设a∈R，若关于x的不等式f（x）≥|$\frac{x}{2}$+a|在R上恒成立，则a的取值范围是（ ）
| A． | [-$\frac{47}{16}$，2] | B． | [-$\frac{47}{16}$，$\frac{39}{16}$] | C． | [-2$\sqrt{3}$，2] | D． | [-2$\sqrt{3}$，$\frac{39}{16}$] |