题目内容
15.已知F1,F2分别是双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的两个焦点,若在双曲线上存在点P满足2|$\overrightarrow{P{F}_{1}}+\overrightarrow{P{F}_{2}}$|≤|$\overrightarrow{{F}_{1}{F}_{2}}$|,则双曲线C的离心率的取值范围是( )| A. | (1,$\sqrt{2}$] | B. | (1,2] | C. | [$\sqrt{2}$,+∞) | D. | [2,+∞) |
分析 运用向量的中点表示,可得$\overrightarrow{PO}$=$\frac{1}{2}$($\overrightarrow{P{F}_{1}}$+$\overrightarrow{P{F}_{2}}$),结合双曲线的范围,可得2c≥4a,再由离心率公式,即可得到所求范围.
解答 解:由OP为△PF1F2的边F1F2的中线,可得
$\overrightarrow{PO}$=$\frac{1}{2}$($\overrightarrow{P{F}_{1}}$+$\overrightarrow{P{F}_{2}}$),
由在双曲线上存在点P满足2|$\overrightarrow{P{F}_{1}}+\overrightarrow{P{F}_{2}}$|≤|$\overrightarrow{{F}_{1}{F}_{2}}$|,
可得4|$\overrightarrow{PO}$|≤2c,
由|$\overrightarrow{PO}$|≥a,可得2c≥4a,
即c≥2a,则e=$\frac{c}{a}$≥2.
故选:D.
点评 本题考查双曲线的离心率的范围,注意运用中点的向量表示,以及双曲线的范围,考查运算能力,属于中档题.

练习册系列答案
相关题目
7.已知△ABC是边长为2的等边三角形,P为平面ABC内一点,则$\overrightarrow{PA}$•($\overrightarrow{PB}$+$\overrightarrow{PC}$)的最小值是( )
| A. | -2 | B. | -$\frac{3}{2}$ | C. | -$\frac{4}{3}$ | D. | -1 |
10.已知X的概率分布为
求Y1=2X-1与Y2=X2的分布列.
| X | -1 | 0 | 1 | 2 |
| Pk | $\frac{1}{8}$ | $\frac{1}{8}$ | $\frac{1}{4}$ | $\frac{1}{2}$ |
5.函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(x)的单调递减区间为( )
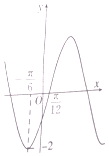

| A. | $(kπ-\frac{π}{6},kπ+\frac{π}{3}),k∈Z$ | B. | $(2kπ-\frac{π}{6},2kπ+\frac{π}{3}),k∈Z$ | ||
| C. | $(2kπ+\frac{π}{3},2kπ+\frac{5π}{6}),k∈Z$ | D. | $(kπ+\frac{π}{3},kπ+\frac{5π}{6}),k∈Z$ |