题目内容
19．已知（1+3x）n的展开式中含有x2的系数是54，则n=4．分析 利用通项公式即可得出．
解答 解：（1+3x）n的展开式中通项公式：Tr+1=${∁}_{n}^{r}$（3x）r=3r${∁}_{n}^{r}$xr．
∵含有x2的系数是54，∴r=2．
∴${3}^{2}{∁}_{n}^{2}$=54，可得${∁}_{n}^{2}$=6，∴$\frac{n（n-1）}{2}$=6，n∈N*．
解得n=4．
故答案为：4．
点评 本题考查了二项式定理的通项公式，考查了推理能力与计算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
5．若双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线被圆（x-2）2+y2=4所截得的弦长为2，则C的离心率为（ ）
| A． | 2 | B． | $\sqrt{3}$ | C． | $\sqrt{2}$ | D． | $\frac{2\sqrt{3}}{3}$ |
10．已知集合P={x|-1＜x＜1}，Q={x|0＜x＜2}，那么P∪Q=（ ）
| A． | （-1，2） | B． | （0，1） | C． | （-1，0） | D． | （1，2） |
7．已知△ABC是边长为2的等边三角形，P为平面ABC内一点，则$\overrightarrow{PA}$•（$\overrightarrow{PB}$+$\overrightarrow{PC}$）的最小值是（ ）
| A． | -2 | B． | -$\frac{3}{2}$ | C． | -$\frac{4}{3}$ | D． | -1 |
14．
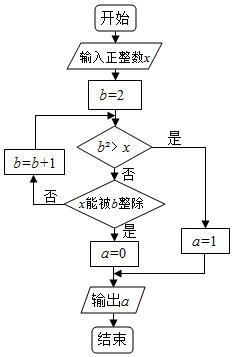执行两次如图所示的程序框图，若第一次输入的x值为7，第二次输入的x值为9，则第一次，第二次输出的a值分别为（ ）
执行两次如图所示的程序框图，若第一次输入的x值为7，第二次输入的x值为9，则第一次，第二次输出的a值分别为（ ）| A． | 0，0 | B． | 1，1 | C． | 0，1 | D． | 1，0 |
11．
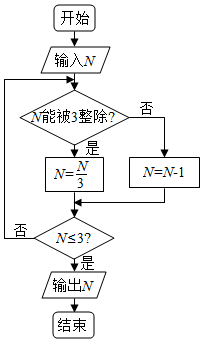阅读右面的程序框图，运行相应的程序，若输入N的值为24，则输出N的值为（ ）
阅读右面的程序框图，运行相应的程序，若输入N的值为24，则输出N的值为（ ）| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
