题目内容
已知f(x)=xlnx.
(1)若不等式c<f(x)恒成立,求c的取值范围;
(2)令f0(x)=f′(x),f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x)=fn′(x);n是正整数;
①写出函数f1(x)、f2(x)、f3(x)、f4(x)的表达式,由此猜想fn(x)(n∈N*)的表达式;
②用数学归纳法证明你的结论.
(1)若不等式c<f(x)恒成立,求c的取值范围;
(2)令f0(x)=f′(x),f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x)=fn′(x);n是正整数;
①写出函数f1(x)、f2(x)、f3(x)、f4(x)的表达式,由此猜想fn(x)(n∈N*)的表达式;
②用数学归纳法证明你的结论.
考点:数学归纳法,函数恒成立问题,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)求出函数的定义域,求出函数的导函数,研究出原函数在定义域上的单调性即可求出函数f(x)在定义域上的最小值,即可.
(2)①通过求解函数的导数,直接得到函数f1(x)、f2(x)、f3(x)、f4(x)的表达式,然后猜想fn(x)(n∈N*)的表达式.
②利用数学归纳法的证明步骤,证明即可.
(2)①通过求解函数的导数,直接得到函数f1(x)、f2(x)、f3(x)、f4(x)的表达式,然后猜想fn(x)(n∈N*)的表达式.
②利用数学归纳法的证明步骤,证明即可.
解答:
解:(1)函数的定义域是(0,+∞)
由f(x)=xlnx,可得f'(x)=lnx+1,(2分)
当x∈(0,
)时,f'(x)<0,f(x)单调递减;
当x∈(
,+∞)时,f'(x)>0,f(x)单调递增.
所以函数f(x)在(0,+∞)上的最小值为:f(
)=-
.
不等式c<f(x)成立,∴c<f(x)min,∴c<-
…(5分)
(2)①f0(x)=f'(x)=1+lnx,
∴f1(x)=f′0(x)=
,f2(x)=f′1(x)=-
,f3(x)=f′2(x)=
=
,f4(x)=f′3(x)=
=-
,…(6分)
猜想fn(x)=(-1)n+1•
…(8分)
证明:(1°)n=1时,f1(x)=(1+lnx)′=x-1=
,∴猜想成立;…(9分)
(2°)设n=k时结论成立即:fk(x)=(-1)k+1•
;
n=k+1时有:fk+1(x)=f′k(x)=[(-1)k+1•(k-1)!x-k]′=(-1)k+1(k-1)!•(-k)x-k-1=(-1)(k+1)+1•
∴n=k+1时结论成立;(11分),
综上由(1°)(2°)可知fn(x)=(-1)n+1•
对任意正整数成立.(12分)
由f(x)=xlnx,可得f'(x)=lnx+1,(2分)
当x∈(0,
| 1 |
| e |
当x∈(
| 1 |
| e |
所以函数f(x)在(0,+∞)上的最小值为:f(
| 1 |
| e |
| 1 |
| e |
不等式c<f(x)成立,∴c<f(x)min,∴c<-
| 1 |
| e |
(2)①f0(x)=f'(x)=1+lnx,
∴f1(x)=f′0(x)=
| 1 |
| x |
| 2 |
| x2 |
| 2•3 |
| x3 |
| 3! |
| x3 |
| -2•3•4 |
| x4 |
| 4! |
| x4 |
猜想fn(x)=(-1)n+1•
| (n-1)! |
| xn |
证明:(1°)n=1时,f1(x)=(1+lnx)′=x-1=
| 1 |
| x |
(2°)设n=k时结论成立即:fk(x)=(-1)k+1•
| (k-1)! |
| xk |
n=k+1时有:fk+1(x)=f′k(x)=[(-1)k+1•(k-1)!x-k]′=(-1)k+1(k-1)!•(-k)x-k-1=(-1)(k+1)+1•
| k! |
| xk+1 |
∴n=k+1时结论成立;(11分),
综上由(1°)(2°)可知fn(x)=(-1)n+1•
| (n-1)! |
| xn |
点评:本题考查函数的导数判断函数的单调性最值的求法,数学归纳法的应用,考查逻辑推理能力以及计算能力.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
已知等差数列2,7,…,则a5=( )
| A、22 | B、15 | C、7 | D、2 |
角θ的终边经过点P(2,-1),则sinθ=( )
| A、2 | ||||
| B、-1 | ||||
C、
| ||||
D、-
|
抛掷3个骰子,当至少一个5点或一个6点出现时,就说这次试验成功,则在54次试验中成功次数n的期望为( )
| A、19 | B、27 | C、54 | D、38 |
 如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PB,且侧面PAB⊥平面ABCD,点E是棱AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PB,且侧面PAB⊥平面ABCD,点E是棱AB的中点.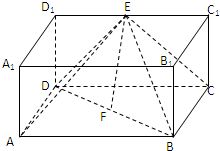 在长方体ABCD-A1B1C1D1中,DC=2DD1,E,F分别为棱C1D1,BD的中点.
在长方体ABCD-A1B1C1D1中,DC=2DD1,E,F分别为棱C1D1,BD的中点.