题目内容

在△ABC中，已知acosA+bcosB=ccosC，a=2bcosC，试判断△ABC的形状．
考点：余弦定理,正弦定理
专题：计算题,解三角形
分析：由a=2bcosC及正弦定理可得，2sinBcosC=sinA=sin（B+C）=sinBcosC+cosBsinC，由此可推得B=C，b=c，再由acosA+bcosB=ccosC，可推得A=
π
2
．
解答： 解：∵a=2bcosC，由正弦定理可得，
2sinBcosC=sinA=sin（B+C）=sinBcosC+cosBsinC，
∴sinBcosC-cosBsinC=0，即sin（B-C）=0，
∴B-C=0，∴B=C，∴b=c，
∴bcosB=ccosC，
∵acosA+bcosB=ccosC，∴acosA=0，
∵a≠0，∴cosA=0，∴A=
π
2
，
∴△ABC是等腰直角三角形．
点评：本题考查正弦定理、余弦定理，考查和角公式，判断三角形形状的基本方法是“化边”或“化角”．
练习册系列答案
相关题目
下列函数 ①y=x+
1
x
（x≥2）；②y=tanx+
1
tanx
；③y=x-3+
1
x-3
；④y=
x2+2
+
1
x2+2
．其中最小值为2的有（　　）
A、0个B、1个C、2个D、3个
设函数f（x）是定义在区间D上的函数，任给x1，x2∈D，且x1≠x2，都有f（
x1+x2
2
）＞
f(x1)+f(x2)
2
，则称函数f（x）为区间D上的严格凸函数．现给出下列命题：
①函数y=log2x与函数y=-x2在区间（0，+∞）上均为严格凸函数；
②函数y=2x与y=tanx在（-1，1）均不为严格凸函数；
③一定存在实数k，使得函数y=x+
k
x
在区间（-∞，0）上为严格凸函数．
其中正确的命题个数为（　　）
A、0个B、1个C、2个D、3个
设函数f（x）=x2+ax-lnx（a∈R）．
（Ⅰ）若a=1，求函数f（x）的单调区间；
（Ⅱ）若函数f（x）在区间（0，1]上是减函数，求实数a的取值范围；
（Ⅲ）过坐标原点O作曲线y=f（x）的切线，证明：切线有且仅有一条，且切点的横坐标恒为1．
已知f（x）=xlnx．
（1）若不等式c＜f（x）恒成立，求c的取值范围；
（2）令f0（x）=f′（x），f1（x）=f0′（x），f2（x）=f1′（x），…，fn+1（x）=fn′（x）；n是正整数；
①写出函数f1（x）、f2（x）、f3（x）、f4（x）的表达式，由此猜想fn（x）（n∈N*）的表达式；
②用数学归纳法证明你的结论．
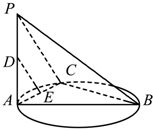如图，已知AB是圆的直径，PA垂直圆所在的平面，C是圆上任一点，D是线段PA的中点，E是线段AC上的一点．
求证：（Ⅰ）若E为线段AC中点，则DE∥平面PBC；
（Ⅱ）无论E在AC何处，都有BC⊥DE．
若正数a，b，c满足a+b+c=1．
（1）求证：
1
3
≤a2+b2+c2＜1；
（2）求
1
2a+1
+
1
2b+1
+
1
2c+1
的最小值．
某市居民2009～2013年货币收入x与购买商品支出Y的统计资料如下表所示：
（ 单　位：亿元）
年份 2009 2010 2011 2012 2013
货币收入x 40 42 46 47 50
购买商品支出Y 33 34 37 40 41
（Ⅰ）画出散点图，判断x与Y是否具有相关关系；
（Ⅱ）已知
b
=0.84，请写出Y对x的回归直线方程y=
b
x+
a
；并估计货币收入为52（亿元）时，购买商品支出大致为多少亿元？
已知|z|2+（z+
.
z
）i=
3-i
2+i
，其中
.
z
是z的共轭复数，求复数z．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网