题目内容
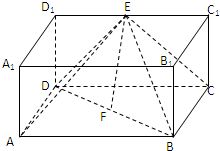 在长方体ABCD-A1B1C1D1中,DC=2DD1,E,F分别为棱C1D1,BD的中点.
在长方体ABCD-A1B1C1D1中,DC=2DD1,E,F分别为棱C1D1,BD的中点.(Ⅰ)求证:EF∥平面BCC1;
(Ⅱ)求证面ADE⊥面BCE.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)取BC的中点为G,连FG,GC1,由E,F分别为棱C1D1,BD的中点推断出FG∥DC,且FG=
DC,EC1∥DC,且EC1=
DC,进而可知EC1∥FG,且EC1=FG推断出FGC1E为平行四边形,继而可知EF∥GC1,利用线面平行的判定定理推断出EF∥平面BCC1
(Ⅱ)由DC=2DD1,E分别为棱C1D1的中点,推断出D1D=D1E,又∠DD1E=90°,进而可求得∠D1ED=45°,同理∠C1EC=45°,进而可知∠DEC=90°.即DE⊥EC,由BC⊥面DC1,又DE?面DC1,推断出BC⊥DE.最后根据面面垂直的判定定理知面ADE⊥面BCE.
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)由DC=2DD1,E分别为棱C1D1的中点,推断出D1D=D1E,又∠DD1E=90°,进而可求得∠D1ED=45°,同理∠C1EC=45°,进而可知∠DEC=90°.即DE⊥EC,由BC⊥面DC1,又DE?面DC1,推断出BC⊥DE.最后根据面面垂直的判定定理知面ADE⊥面BCE.
解答:
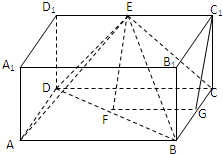 解:(Ⅰ)取BC的中点为G,连FG,GC1,
解:(Ⅰ)取BC的中点为G,连FG,GC1,
∵E,F分别为棱C1D1,BD的中点
∴FG∥DC,且FG=
DC,EC1∥DC,且EC1=
DC,
∴EC1∥FG,且EC1=FG
∴FGC1E为平行四边形,∴EF∥GC1
∵EF⊆平面BCC1,GC1⊆平面BCC1,
∴EF∥平面BCC1
(Ⅱ)∵DC=2DD1,E分别为棱C1D1的中点,
∴D1D=D1E,
又∵∠DD1E=90°,
∴∠D1ED=45°,同理∠C1EC=45°,
∴∠DEC=90°.即DE⊥EC,
∵BC⊥面DC1,又∵DE?面DC1,
∴BC⊥DE.
∵BC∩CE=C,
∴DE⊥面BCE.
∵DE?面ADE,
∴面ADE⊥面BCE.
 解:(Ⅰ)取BC的中点为G,连FG,GC1,
解:(Ⅰ)取BC的中点为G,连FG,GC1,∵E,F分别为棱C1D1,BD的中点
∴FG∥DC,且FG=
| 1 |
| 2 |
| 1 |
| 2 |
∴EC1∥FG,且EC1=FG
∴FGC1E为平行四边形,∴EF∥GC1
∵EF⊆平面BCC1,GC1⊆平面BCC1,
∴EF∥平面BCC1
(Ⅱ)∵DC=2DD1,E分别为棱C1D1的中点,
∴D1D=D1E,
又∵∠DD1E=90°,
∴∠D1ED=45°,同理∠C1EC=45°,
∴∠DEC=90°.即DE⊥EC,
∵BC⊥面DC1,又∵DE?面DC1,
∴BC⊥DE.
∵BC∩CE=C,
∴DE⊥面BCE.
∵DE?面ADE,
∴面ADE⊥面BCE.
点评:本题主要考查了面面垂直的判定定理,线面平行的判定定理的应用.在进行面面垂直的判定过程中,证明线面垂直是关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
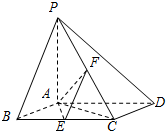 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.