题目内容

抛掷3个骰子，当至少一个5点或一个6点出现时，就说这次试验成功，则在54次试验中成功次数n的期望为（　　）
A、19B、27C、54D、38
考点：离散型随机变量的期望与方差
专题：计算题,概率与统计
分析：由题意知试验中的事件是相互独立的，事件发生的概率是相同的，得到成功次数n服从二项分布，根据二项分布的期望公式得到结果．
解答： 解：∵成功次数n服从二项分布，
每次试验成功的概率为1-
2
3
×
2
3
×
2
3
=
19
27
，
∴在54次试验中，成功次数n的期望为
19
27
×54=38．
故选：D．
点评：二项分布要满足的条件：每次试验中，事件发生的概率是相同的，各次试验中的事件是相互独立的，每次试验只要两种结果，要么发生要么不发生，随机变量是这n次独立重复试验中事件发生的次数．
练习册系列答案
相关题目
已知|
a
|=3，|
b
|=4，（
a
+
b
）•（
a
+3
b
）=33，则
a
与
b
的夹角为（　　）
A、30°B、60°
C、120°D、150°
已知函数f（x）=1-ex，则f′（0）=（　　）
A、0B、-1C、eD、1
设函数f（x）是定义在区间D上的函数，任给x1，x2∈D，且x1≠x2，都有f（
x1+x2
2
）＞
f(x1)+f(x2)
2
，则称函数f（x）为区间D上的严格凸函数．现给出下列命题：
①函数y=log2x与函数y=-x2在区间（0，+∞）上均为严格凸函数；
②函数y=2x与y=tanx在（-1，1）均不为严格凸函数；
③一定存在实数k，使得函数y=x+
k
x
在区间（-∞，0）上为严格凸函数．
其中正确的命题个数为（　　）
A、0个B、1个C、2个D、3个
方程
x2
4-t
+
y2
t-1
=1表示曲线C，给出下列四个命题，其中正确的命题个数是（　　）
①若曲线C为椭圆，则1＜t＜4
②若曲线C为双曲线，则t＜1或t＞4
③曲线C不可能是圆
④若曲线C表示焦点在X轴上的椭圆，则1＜t＜
5
2
．
A、1B、2C、3D、4
设函数f（x）=x2+ax-lnx（a∈R）．
（Ⅰ）若a=1，求函数f（x）的单调区间；
（Ⅱ）若函数f（x）在区间（0，1]上是减函数，求实数a的取值范围；
（Ⅲ）过坐标原点O作曲线y=f（x）的切线，证明：切线有且仅有一条，且切点的横坐标恒为1．
已知f（x）=xlnx．
（1）若不等式c＜f（x）恒成立，求c的取值范围；
（2）令f0（x）=f′（x），f1（x）=f0′（x），f2（x）=f1′（x），…，fn+1（x）=fn′（x）；n是正整数；
①写出函数f1（x）、f2（x）、f3（x）、f4（x）的表达式，由此猜想fn（x）（n∈N*）的表达式；
②用数学归纳法证明你的结论．
若正数a，b，c满足a+b+c=1．
（1）求证：
1
3
≤a2+b2+c2＜1；
（2）求
1
2a+1
+
1
2b+1
+
1
2c+1
的最小值．
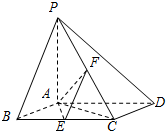如图，已知四棱锥P-ABCD，底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E，F分别是BC，PC的中点．
（1）证明：AE⊥PD；
（2）若PA=AB=2，求二面角E-AF-C的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网