题目内容
用数学归纳法证明:
+
+
+…+
>
(n≥2,n∈N*)
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+3 |
| 1 |
| 2n |
| 13 |
| 24 |
考点:数学归纳法
专题:点列、递归数列与数学归纳法
分析:直接利用数学归纳法证明问题的步骤,证明不等式即可.
解答:
证明:(1)当n=2时,
+
=
,
>
命题成立.
(2)假设当n=k时,
+
+
+…+
>
成立
当n=k+1时,
+
+…+
+
+
=
+
+
+…+
+
+
-
>
+
+
-
,
∵
+
-
=
>0,
∴
+
+
+…+
>
,
当n=k+1时命题成立.
所以对于任意n≥2,n∈N*都成立.
| 1 |
| 2+1 |
| 1 |
| 2+2 |
| 14 |
| 24 |
| 14 |
| 24 |
| 13 |
| 24 |
(2)假设当n=k时,
| 1 |
| k+1 |
| 1 |
| k+2 |
| 1 |
| k+3 |
| 1 |
| 2k |
| 13 |
| 24 |
当n=k+1时,
| 1 |
| k+2 |
| 1 |
| k+3 |
| 1 |
| 2k |
| 1 |
| 2k+1 |
| 1 |
| 2k+2 |
| 1 |
| k+1 |
| 1 |
| k+2 |
| 1 |
| k+3 |
| 1 |
| 2k |
| 1 |
| 2k+1 |
| 1 |
| 2k+2 |
| 1 |
| k+1 |
| 13 |
| 24 |
| 1 |
| 2k+1 |
| 1 |
| 2k+2 |
| 1 |
| k+1 |
∵
| 1 |
| 2k+1 |
| 1 |
| 2k+2 |
| 1 |
| k+1 |
| 1 |
| 2(2k+1)(k+1) |
∴
| 1 |
| (k+1)+1 |
| 1 |
| (k+1)+2 |
| 1 |
| (k+1)+3 |
| 1 |
| 2(k+1) |
| 13 |
| 24 |
当n=k+1时命题成立.
所以对于任意n≥2,n∈N*都成立.
点评:本题考查数学归纳法证明含自然数n的表达式的证明方法,注意n=k+1的证明时,必须用上假设.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
已知函数f(x)=1-ex,则f′(0)=( )
| A、0 | B、-1 | C、e | D、1 |

 某市居民2009~2013年货币收入x与购买商品支出Y的统计资料如下表所示:
某市居民2009~2013年货币收入x与购买商品支出Y的统计资料如下表所示:
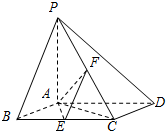 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.