题目内容
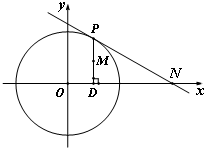 如图,在圆O:x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足.设M为线段PD的中点.
如图,在圆O:x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足.设M为线段PD的中点.(Ⅰ)当点P在圆O上运动时,求点M的轨迹E的方程;
(Ⅱ)若圆O在点P处的切线与x轴交于点N,试判断直线MN与轨迹E的位置关系.
考点:直线与圆锥曲线的综合问题,轨迹方程
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)设M(x,y),则P(x,2y).由点P在圆x2 +y2=4上,能求出点M的轨迹E的方程.
(Ⅱ)当直线PN的斜率不存在时,直线MN与轨迹E相切;当直线PN的斜率存在时,设PN的方程为y=kx+t,由直线PN与圆O相切,得到t2-4k2-4=0,直线MN的方程为y=
(kx+t),由
,得(1+k2)x22-4=0,由此利用根的判别式得到直线MN与轨迹E相切.
(Ⅱ)当直线PN的斜率不存在时,直线MN与轨迹E相切;当直线PN的斜率存在时,设PN的方程为y=kx+t,由直线PN与圆O相切,得到t2-4k2-4=0,直线MN的方程为y=
| 1 |
| 2 |
|
解答:
满分(13分).
解:(Ⅰ)设M(x,y),则P(x,2y).
∵点P在圆x2 +y2=4上,∴x2 +(2y)2=4,
∴点M的轨迹E的方程为
+y2=1.…(4分)
(Ⅱ)(i) 当直线PN的斜率不存在时,
直线MN的方程为x=2或x=-2.与轨迹E相切;
(ii)当直线PN的斜率存在时,设PN的方程为y=kx+t,k≠0,
∵直线PN与圆O相切,∴
=2,即t2-4k2-4=0.…(7分)
又直线MN的斜率等于
,点N的坐标为(-
,0).
∴直线MN的方程为y=
(x+
),即y=
(kx+t). …(9分)
由
,得(1+k2)x22-4=0.
∵△=(2kt)2-4(1+k2)(t2-4)
=4k2(t2-4k2-4)=0.
故直线MN与轨迹E相切.
综上(i)(ii)知,直线MN与轨迹E相切. …(13分)
解:(Ⅰ)设M(x,y),则P(x,2y).
∵点P在圆x2 +y2=4上,∴x2 +(2y)2=4,
∴点M的轨迹E的方程为
| x2 |
| 4 |
(Ⅱ)(i) 当直线PN的斜率不存在时,
直线MN的方程为x=2或x=-2.与轨迹E相切;
(ii)当直线PN的斜率存在时,设PN的方程为y=kx+t,k≠0,
∵直线PN与圆O相切,∴
| |t| | ||
|
又直线MN的斜率等于
| k |
| 2 |
| t |
| k |
∴直线MN的方程为y=
| k |
| 2 |
| t |
| k |
| 1 |
| 2 |
由
|
∵△=(2kt)2-4(1+k2)(t2-4)
=4k2(t2-4k2-4)=0.
故直线MN与轨迹E相切.
综上(i)(ii)知,直线MN与轨迹E相切. …(13分)
点评:本小题考查椭圆的标准方程与性质、直线与圆锥曲线的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在平面直角坐标系xOy中,椭圆
如图,在平面直角坐标系xOy中,椭圆 已知函数f(x)=sin(ωx+φ)(ω>0,φ<
已知函数f(x)=sin(ωx+φ)(ω>0,φ<