题目内容
已知函数f（x）=2sin2（
+x）+
cos2x+a，x∈R．且f（x）在[-
，
]上的最小值是-1
（1）求函数f（x）的最小正周期及a的值；
（2）在△ABC中，若f（C）=
，2sinB=cos（A-C）-cos（A+C），求tanA的值．
| π |
| 4 |
| 3 |
| π |
| 4 |
| π |
| 4 |
（1）求函数f（x）的最小正周期及a的值；
（2）在△ABC中，若f（C）=
| 3 |
考点：三角函数中的恒等变换应用,三角函数的周期性及其求法
专题：三角函数的图像与性质
分析：（1）首先，利用二倍角公式化简函数解析式f（x）=2sin（2x+
）+a+1，然后借助于周期公式和三角函数的性质求解；
（2）利用f（C）=
，求解C的值，然后，结合2sinB=cos（A-C）-cos（A+C），得到cosA=（1-
）sinA，最后，求解tanA的值．
| π |
| 3 |
（2）利用f（C）=
| 3 |
| 3 |
解答：
解：（1）∵函数f（x）=2sin2（
+x）+
cos2x+a
∴f（x）=1-cos（
+2x）+
cos2x+a
=sin2x+
cos2x+a+1，
=2sin（2x+
）+a+1，
∴f（x）=2sin（2x+
）+a+1，
∴T=
=π，
∴函数f（x）的最小正周期π，
∵x∈[-
，
]，
∴（2x+
）∈[-
，
]，
∴2sin（2x+
）∈[-1，2]，
∴f（x）=2sin（2x+
）+a+1∈[a，3+a]，
∵f（x）在[-
，
]上的最小值是-1
∴a=-1，
∴a的值-1．
（2）根据（1），f（x）=2sin（2x+
），
∴f（C）=2sin（2C+
）=
，
∴sin（2C+
）=
，
∴2C+
=
，
∴C=
，
∵2sinB=cos（A-C）-cos（A+C），
∴2sinB=2sinAsinC，
∴2sin（
-A）=sinA，
∴2sin（A+
）=sinA，
∴cosA=（1-
）sinA，
∴tanA=
=
=-
．
| π |
| 4 |
| 3 |
∴f（x）=1-cos（
| π |
| 2 |
| 3 |
=sin2x+
| 3 |
=2sin（2x+
| π |
| 3 |
∴f（x）=2sin（2x+
| π |
| 3 |
∴T=
| 2π |
| 2 |
∴函数f（x）的最小正周期π，
∵x∈[-
| π |
| 4 |
| π |
| 4 |
∴（2x+
| π |
| 3 |
| π |
| 6 |
| 5π |
| 6 |
∴2sin（2x+
| π |
| 3 |
∴f（x）=2sin（2x+
| π |
| 3 |
∵f（x）在[-
| π |
| 4 |
| π |
| 4 |
∴a=-1，
∴a的值-1．
（2）根据（1），f（x）=2sin（2x+
| π |
| 3 |
∴f（C）=2sin（2C+
| π |
| 3 |
| 3 |
∴sin（2C+
| π |
| 3 |
| ||
| 2 |
∴2C+
| π |
| 3 |
| 2π |
| 3 |
∴C=
| π |
| 6 |
∵2sinB=cos（A-C）-cos（A+C），
∴2sinB=2sinAsinC，
∴2sin（
| 5π |
| 6 |
∴2sin（A+
| π |
| 6 |
∴cosA=（1-
| 3 |
∴tanA=
| sinA |
| cosA |
| 1 | ||
1-
|
1+
| ||
| 2 |
点评：本题综合考查了二倍角公式、诱导公式、和差化积公式等知识，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
已知函数f（x）=Asin（wx+φ）+b，（w＞0），|φ|＜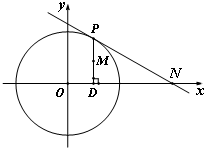
如图，在圆O：x2+y2=4上任取一点P，过点P作x轴的垂线段PD，D为垂足．设M为线段PD的中点．