题目内容
将函数y=cos(
π-ωx)(ω>0)的图象向左平移
个单位后,得到函数y=sin(2x+φ)的图象,则函数y=sin(2x+φ)的一个对称中心为( )
| 3 |
| 2 |
| π |
| 3 |
A、(
| ||
B、(
| ||
C、(
| ||
D、(
|
考点:余弦函数的对称性
专题:三角函数的图像与性质
分析:由题意得y=sin(ωx+
-π)=sin(2x+φ),可解得函数y=sin(2x+φ)的解析式为y=sin(2x-
),从而可求其对称中心.
| ωπ |
| 3 |
| π |
| 3 |
解答:
解:由题意得y=cos(
π-ωx)(ω>0)的图象向左平移
个单位后,
得到函数y=cos[
-ω(x+
)]=sin(ωx+
-π)=sin(2x+φ),
故可解得:ω=2,φ=-
,
故函数y=sin(2x+φ)的解析式为y=sin(2x-
),
由2x-
=kπ,即x=
+
,即函数的对称中心为(
+
,0),k∈Z,
当k=0时有函数的对称中心为(
,0),
故选:B.
| 3 |
| 2 |
| π |
| 3 |
得到函数y=cos[
| 3π |
| 2 |
| π |
| 3 |
| ωπ |
| 3 |
故可解得:ω=2,φ=-
| π |
| 3 |
故函数y=sin(2x+φ)的解析式为y=sin(2x-
| π |
| 3 |
由2x-
| π |
| 3 |
| π |
| 6 |
| kπ |
| 2 |
| π |
| 6 |
| kπ |
| 2 |
当k=0时有函数的对称中心为(
| π |
| 6 |
故选:B.
点评:本题主要考查了余弦函数的对称性,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知f(x6)=log2x,则f(8)=( )
A、
| ||
| B、8 | ||
| C、18 | ||
D、
|
全称命题“?x∈R,x2+2x+3≥0”的否定是( )
| A、?x∈R,x2+2x+3<0 |
| B、?x∉R,x2+2x+3≥0 |
| C、?x∈R,x2+2x+3≤0 |
| D、?x∈R,x2+2x+3<0 |
不等式(x-1)(x+2)≤0的解集是( )
| A、[1,2] |
| B、[-1,2] |
| C、[-2,1] |
| D、(-∞,-2]∪[1,+∞) |
直线x+
y+2=0的倾斜角为( )
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
在高为150米的山顶上,测得山下一铁塔的塔顶和塔底的俯角分别为30°和60°,则铁塔的高度为( )
| A、20米 | ||
| B、100米 | ||
| C、50米 | ||
D、50
|
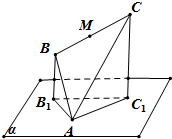 如图,边长为4的正△ABC顶点A在平面α上,B,C在平面α的同侧,且点C到平面α的距离是点B到平面α的距离的
如图,边长为4的正△ABC顶点A在平面α上,B,C在平面α的同侧,且点C到平面α的距离是点B到平面α的距离的