题目内容
已知函数f(x)=lg(x2-5x-6),则f(x)的增区间为 .
考点:复合函数的单调性
专题:函数的性质及应用
分析:由对数式的真数大于0求得函数的定义域,再求出定义域内二次函数的增区间得答案.
解答:
解:由x2-5x-6>0,得x<-1或x>6,
∵对数函数y=lgt为增函数,
∴函数t=x2-5x-6的增区间即为f(x)的增区间,为(6,+∞).
故答案为:(6,+∞).
∵对数函数y=lgt为增函数,
∴函数t=x2-5x-6的增区间即为f(x)的增区间,为(6,+∞).
故答案为:(6,+∞).
点评:本题考查复合函数的单调性,复合的两个函数同增则增,同减则减,一增一减则减,注意对数函数的定义域是求解的前提,考查学生发现问题解决问题的能力,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在高为150米的山顶上,测得山下一铁塔的塔顶和塔底的俯角分别为30°和60°,则铁塔的高度为( )
| A、20米 | ||
| B、100米 | ||
| C、50米 | ||
D、50
|
函数f(x)是定义在R上的奇函数,并且当x∈(0,+∞)时,f(x)=lnx,那么,f(-e2)=( )
| A、-2 | B、2 | C、1 | D、无法确定 |
下列对应中,是映射的个数为( )


| A、0 | B、1 | C、2 | D、3 |
已知函数f(x)=xa,且满足f(9)=3,则f(100)=( )
| A、10 | B、100 |
| C、1000 | D、10000 |
某算法程序框图如图所示,若a=
,b=3
,c=log23,则x=( )

| 3 |
| 2 |
| 1 |
| 3 |

A、
| ||
| B、a | ||
| C、b | ||
| D、c |
设a=log23,b=log32,c=log2(log32),则( )
| A、c<b<a |
| B、b<a<c |
| C、b<c<a |
| D、c<a<b |
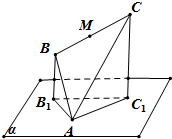 如图,边长为4的正△ABC顶点A在平面α上,B,C在平面α的同侧,且点C到平面α的距离是点B到平面α的距离的
如图,边长为4的正△ABC顶点A在平面α上,B,C在平面α的同侧,且点C到平面α的距离是点B到平面α的距离的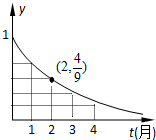 如图,是某受污染的湖泊在自然净化过程中,某种有害物质的剩留量y与净化时间t(月)的近似函数关系:y=at(a>0,a≠1,t≥0),有以下叙述:
如图,是某受污染的湖泊在自然净化过程中,某种有害物质的剩留量y与净化时间t(月)的近似函数关系:y=at(a>0,a≠1,t≥0),有以下叙述: