题目内容
已知函数f(x)=a•2x-2-x,函数g(x)的图象与f(x)的图象关于y轴对称.
(Ⅰ)求g(x)的解析式;
(Ⅱ)若对任意x∈R,不等式f(x)+g(x)-1≥0恒成立,求实数a的取值范围.
(Ⅰ)求g(x)的解析式;
(Ⅱ)若对任意x∈R,不等式f(x)+g(x)-1≥0恒成立,求实数a的取值范围.
考点:函数奇偶性的性质,函数恒成立问题
专题:函数的性质及应用
分析:(Ⅰ)设p(x,y)为g(x)上任意一点,则p(x,y)关于y轴对称点为p′(-x,y),由题意知p′(-x,y)在f(x)图象上,代入可得g(x)=a•2-x-2x;
(Ⅱ)由题意可得a(2-x+2x)-(2-x+2x)-1≥0,解得a≥1+
(x∈R),令y=t+
,其中t=2x>0,易知y在(0,1)单调递减,在(1,+∞)单调递增,即可推得ymin=2,进而求得实数a的取值范围.
(Ⅱ)由题意可得a(2-x+2x)-(2-x+2x)-1≥0,解得a≥1+
| 1 |
| 2x+2-x |
| 1 |
| t |
解答:
解:(Ⅰ)设p(x,y)为g(x)上任意一点,则p(x,y)关于y轴对称点为p′(-x,y),
由题意知p′(-x,y)在f(x)图象上,故g(x)=a•2-x-2x.
(Ⅱ)由f(x)+g(x)-1≥0得a(2-x+2x)-(2-x+2x)-1≥0,
∵2-x+2x>0
∴a≥1+
(x∈R)
令y=t+
,其中t=2x>0,易知y在(0,1)单调递减,在(1,+∞)单调递增,
∴当t=1,即x=0时,ymin=2
∴(1+
)max=
.
故有:a≥
.
由题意知p′(-x,y)在f(x)图象上,故g(x)=a•2-x-2x.
(Ⅱ)由f(x)+g(x)-1≥0得a(2-x+2x)-(2-x+2x)-1≥0,
∵2-x+2x>0
∴a≥1+
| 1 |
| 2x+2-x |
令y=t+
| 1 |
| t |
∴当t=1,即x=0时,ymin=2
∴(1+
| 1 |
| 2x+2-x |
| 3 |
| 2 |
故有:a≥
| 3 |
| 2 |
点评:本题主要考察了函数奇偶性的性质,函数恒成立问题及解法,属于中档题.

练习册系列答案
相关题目
不等式(x-1)(x+2)≤0的解集是( )
| A、[1,2] |
| B、[-1,2] |
| C、[-2,1] |
| D、(-∞,-2]∪[1,+∞) |
若直线y=x+b与曲线x=3-
有公共点,则b的取值范围是( )
| 4y-y2 |
A、[-1-2
| ||||
B、[-3,-1+2
| ||||
C、[-1-2
| ||||
D、[-3,-1+
|
直线kx+y-2=0(k∈R)与圆x2+y2+2x-2y-1=0的位置关系是( )
| A、相交 | B、相切 | C、相离 | D、不确定 |
已知函数f(x)=xa,且满足f(9)=3,则f(100)=( )
| A、10 | B、100 |
| C、1000 | D、10000 |
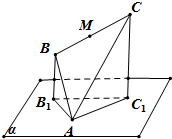 如图,边长为4的正△ABC顶点A在平面α上,B,C在平面α的同侧,且点C到平面α的距离是点B到平面α的距离的
如图,边长为4的正△ABC顶点A在平面α上,B,C在平面α的同侧,且点C到平面α的距离是点B到平面α的距离的