题目内容
对于任意实数a,点P(a,2-a)与圆C:x2+y2=2的位置关系的所有可能是 .
考点:点与圆的位置关系
专题:计算题,直线与圆
分析:求出点P(a,2-a)到圆心C的距离,与圆的半径比较,我们可以得出结论.
解答:
解:将点P(a,2-a)代入圆的方程的左边,可得x2+y2=a2+(2-a)2=2(a-1)2+2≥2
即点P(a,2-a)到圆心C的距离大于等于半径
∴点P(a,2-a)在圆上或圆外.
故答案为:在圆上或圆外.
即点P(a,2-a)到圆心C的距离大于等于半径
∴点P(a,2-a)在圆上或圆外.
故答案为:在圆上或圆外.
点评:点与圆的位置关系,只需要利用点与圆心的距离与圆的半径比较,这是我们常用的方法.

练习册系列答案
相关题目
已知f(x6)=log2x,则f(8)=( )
A、
| ||
| B、8 | ||
| C、18 | ||
D、
|
若直线y=x+b与曲线x=3-
有公共点,则b的取值范围是( )
| 4y-y2 |
A、[-1-2
| ||||
B、[-3,-1+2
| ||||
C、[-1-2
| ||||
D、[-3,-1+
|
直线kx+y-2=0(k∈R)与圆x2+y2+2x-2y-1=0的位置关系是( )
| A、相交 | B、相切 | C、相离 | D、不确定 |
在高为150米的山顶上,测得山下一铁塔的塔顶和塔底的俯角分别为30°和60°,则铁塔的高度为( )
| A、20米 | ||
| B、100米 | ||
| C、50米 | ||
D、50
|
函数f(x)是定义在R上的奇函数,并且当x∈(0,+∞)时,f(x)=lnx,那么,f(-e2)=( )
| A、-2 | B、2 | C、1 | D、无法确定 |
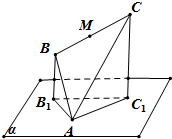 如图,边长为4的正△ABC顶点A在平面α上,B,C在平面α的同侧,且点C到平面α的距离是点B到平面α的距离的
如图,边长为4的正△ABC顶点A在平面α上,B,C在平面α的同侧,且点C到平面α的距离是点B到平面α的距离的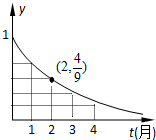 如图,是某受污染的湖泊在自然净化过程中,某种有害物质的剩留量y与净化时间t(月)的近似函数关系:y=at(a>0,a≠1,t≥0),有以下叙述:
如图,是某受污染的湖泊在自然净化过程中,某种有害物质的剩留量y与净化时间t(月)的近似函数关系:y=at(a>0,a≠1,t≥0),有以下叙述: