题目内容
方程lnx=2-x的根所在区间是( )
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
考点:利用导数研究函数的单调性,函数零点的判定定理
专题:导数的综合应用
分析:令f(x)=lnx+x-2,函数在定义域(0,+∞)连续,且f(x)=lnx+x-2在(0,1]单调递增,在(1,+∞)单调递减由零点判定定理可判定函数的零点所在的区间
解答:
解:令f(x)=lnx+x-2,函数在定义域(0,+∞)连续,
∵f′(x)=
+1,
∴f(x)=lnx+x-2在(0,+∞)单调递增.
∵f(1)=-1<0,f(2)=ln2>0,
由零点判定定理可得函数的零点 的区间是(1,2),
故选:C.
∵f′(x)=
| 1 |
| X |
∴f(x)=lnx+x-2在(0,+∞)单调递增.
∵f(1)=-1<0,f(2)=ln2>0,
由零点判定定理可得函数的零点 的区间是(1,2),
故选:C.
点评:本题主要考查了函数的零点判定定理的应用,属于基础性试题.

练习册系列答案
相关题目
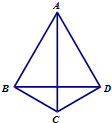 如图,将两个全等的30°的直角三角形ABC和直角三角形ADC拼在一起组成平面四边形ABCD,若
如图,将两个全等的30°的直角三角形ABC和直角三角形ADC拼在一起组成平面四边形ABCD,若| DB |
| DA |
| DC |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知f(x6)=log2x,则f(8)=( )
A、
| ||
| B、8 | ||
| C、18 | ||
D、
|
不等式(x-1)(x+2)≤0的解集是( )
| A、[1,2] |
| B、[-1,2] |
| C、[-2,1] |
| D、(-∞,-2]∪[1,+∞) |
直线x+
y+2=0的倾斜角为( )
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
若直线y=x+b与曲线x=3-
有公共点,则b的取值范围是( )
| 4y-y2 |
A、[-1-2
| ||||
B、[-3,-1+2
| ||||
C、[-1-2
| ||||
D、[-3,-1+
|
函数f(x)是定义在R上的奇函数,并且当x∈(0,+∞)时,f(x)=lnx,那么,f(-e2)=( )
| A、-2 | B、2 | C、1 | D、无法确定 |
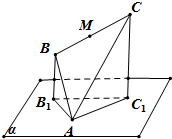 如图,边长为4的正△ABC顶点A在平面α上,B,C在平面α的同侧,且点C到平面α的距离是点B到平面α的距离的
如图,边长为4的正△ABC顶点A在平面α上,B,C在平面α的同侧,且点C到平面α的距离是点B到平面α的距离的