题目内容
一长方体的各顶点均在同一个球面上,且一个顶点上的三条棱长分别为1,
,3,则这个球的表面积为 .
| 6 |
考点:球的体积和表面积
专题:计算题,空间位置关系与距离
分析:求出长方体的对角线的长,就是外接球的直径,然后求出球的表面积.
解答:
解:由题意可知长方体的对角线的长,就是外接球的直径,
所以球的直径:
=4,所以外接球的半径为:2.
所以这个球的表面积:4π×22=16π.
故答案为:16π.
所以球的直径:
| 1+6+9 |
所以这个球的表面积:4π×22=16π.
故答案为:16π.
点评:本题考查球内接多面体,球的体积和表面积的求法,考查计算能力.

练习册系列答案
相关题目
直线x+
y+2=0的倾斜角为( )
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
已知函数f(x)=2xcosx,则函数f(x)的部分图象可以为( )
A、 |
B、 |
C、 |
D、 |
若直线y=x+b与曲线x=3-
有公共点,则b的取值范围是( )
| 4y-y2 |
A、[-1-2
| ||||
B、[-3,-1+2
| ||||
C、[-1-2
| ||||
D、[-3,-1+
|
在高为150米的山顶上,测得山下一铁塔的塔顶和塔底的俯角分别为30°和60°,则铁塔的高度为( )
| A、20米 | ||
| B、100米 | ||
| C、50米 | ||
D、50
|
某算法程序框图如图所示,若a=
,b=3
,c=log23,则x=( )

| 3 |
| 2 |
| 1 |
| 3 |

A、
| ||
| B、a | ||
| C、b | ||
| D、c |
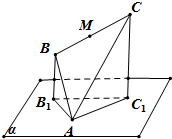 如图,边长为4的正△ABC顶点A在平面α上,B,C在平面α的同侧,且点C到平面α的距离是点B到平面α的距离的
如图,边长为4的正△ABC顶点A在平面α上,B,C在平面α的同侧,且点C到平面α的距离是点B到平面α的距离的