题目内容
14．在△ABC中，AB=8，BC=7，AC=5，则AB边上的高是$\frac{5\sqrt{3}}{2}$．分析 设AB边上的高为h，利用余弦定理可得cosC，sinC，再利用三角形面积计算公式即可得出．
解答 解：设AB边上的高为h，cosC=$\frac{{5}^{2}+{7}^{2}-{8}^{2}}{2×5×7}$=-$\frac{1}{7}$，sinC=$\frac{4\sqrt{3}}{7}$．
∴$\frac{1}{2}×8$h=$\frac{1}{2}×5×7×$$\frac{4\sqrt{3}}{7}$，解得h=$\frac{5\sqrt{3}}{2}$．
故答案为：$\frac{{5\sqrt{3}}}{2}$．
点评 本题考查了余弦定理的应用、三角形面积计算公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
一本好题口算题卡系列答案
相关题目
5．函数f（x）=lnx-$\frac{2}{x-1}$的零点所在的大致区间是（ ）
| A． | （1，2） | B． | （2，3） | C． | （3，4） | D． | （4，5） |
9．从1，2，3，4四个数字中任取两个不同数字，则这两个数字之积小于5的概率为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{5}{6}$ |
19．
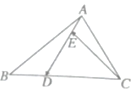如图，在△ABC中，点D在BC边上，且CD=2DB，点E在AD边上，且AD=3AE，则用向量$\overrightarrow{AB}，\overrightarrow{AC}$表示$\overrightarrow{CE}$为（ ）
如图，在△ABC中，点D在BC边上，且CD=2DB，点E在AD边上，且AD=3AE，则用向量$\overrightarrow{AB}，\overrightarrow{AC}$表示$\overrightarrow{CE}$为（ ）| A． | $\overrightarrow{CE}=\frac{2}{9}\overrightarrow{AB}+\frac{8}{9}\overrightarrow{AC}$ | B． | $\overrightarrow{CE}=\frac{2}{9}\overrightarrow{AB}-\frac{8}{9}\overrightarrow{AC}$ | C． | $\overrightarrow{CE}=\frac{2}{9}\overrightarrow{AB}+\frac{7}{9}\overrightarrow{AC}$ | D． | $\overrightarrow{CE}=\frac{2}{9}\overrightarrow{AB}-\frac{7}{9}\overrightarrow{AC}$ |