题目内容
19.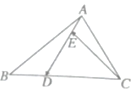 如图,在△ABC中,点D在BC边上,且CD=2DB,点E在AD边上,且AD=3AE,则用向量$\overrightarrow{AB},\overrightarrow{AC}$表示$\overrightarrow{CE}$为( )
如图,在△ABC中,点D在BC边上,且CD=2DB,点E在AD边上,且AD=3AE,则用向量$\overrightarrow{AB},\overrightarrow{AC}$表示$\overrightarrow{CE}$为( )| A. | $\overrightarrow{CE}=\frac{2}{9}\overrightarrow{AB}+\frac{8}{9}\overrightarrow{AC}$ | B. | $\overrightarrow{CE}=\frac{2}{9}\overrightarrow{AB}-\frac{8}{9}\overrightarrow{AC}$ | C. | $\overrightarrow{CE}=\frac{2}{9}\overrightarrow{AB}+\frac{7}{9}\overrightarrow{AC}$ | D. | $\overrightarrow{CE}=\frac{2}{9}\overrightarrow{AB}-\frac{7}{9}\overrightarrow{AC}$ |
分析 根据向量的加减的几何意义和三角形法则即可求出.
解答 解:∵CD=2DB,点E在AD边上,
∴$\overrightarrow{AD}$=$\overrightarrow{AC}$+$\overrightarrow{CD}$=$\overrightarrow{AC}$+$\frac{2}{3}$$\overrightarrow{CB}$=$\overrightarrow{AC}$+$\frac{2}{3}$($\overrightarrow{AB}$-$\overrightarrow{AC}$)=$\frac{1}{3}$$\overrightarrow{AC}$+$\frac{2}{3}$$\overrightarrow{AB}$
∴$\overrightarrow{CE}$=$\overrightarrow{AE}$-$\overrightarrow{AC}$=$\frac{1}{3}$$\overrightarrow{AD}$-$\overrightarrow{AC}$=$\frac{1}{9}$$\overrightarrow{AC}$+$\frac{2}{9}$$\overrightarrow{AB}$-$\overrightarrow{AC}$=$\frac{2}{9}$$\overrightarrow{AB}$-$\frac{8}{9}$$\overrightarrow{AC}$,
故选:B.
点评 本题考查了向量的三角形法则和向量的数乘运算,属于基础题.

练习册系列答案
相关题目
9.已知双曲线${C_1}:\frac{x^2}{6}-\frac{y^2}{2}=1$与双曲线${C_2}:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的离心率相同,且双曲线C2的左、右焦点分别为F1,F2,M是双曲线C2一条渐近线上的某一点,且OM⊥MF2,${S_{△OM{F_2}}}=8\sqrt{3}$,则双曲线C2的实轴长为( )
| A. | 4 | B. | $4\sqrt{3}$ | C. | 8 | D. | $8\sqrt{3}$ |
7.设复数z满足$\frac{i}{1-i}$•z=1,则|z|=( )
| A. | 1 | B. | 5 | C. | $\sqrt{2}$ | D. | 2 |
8.已知集合A={x|y=lgx},B={x|x-1≤0},则A∩B=( )
| A. | (0,1] | B. | (0,1) | C. | (-1,1] | D. | [1,+∞) |
9.将周期为π的函数f(x)=2sin(ωx+$\frac{π}{3}$),(ω>0)的图象向右平移φ个单位,所得图象关于y轴对称,则φ的最小正值是( )
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
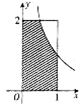 如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数$y=\frac{1}{x}(x>0)$图象下方的阴影部分区域,则阴影部分E的面积为1+ln2.
如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数$y=\frac{1}{x}(x>0)$图象下方的阴影部分区域,则阴影部分E的面积为1+ln2.