题目内容
4.已知函数f(x)=|x+1|+|x-3|.(1)求不等式f(x)<6的解集;
(2)若关于x的不等式f(x)≥|2a+1|不恒成立,求实数a的取值范围.
分析 (1)分类讨论,即可解不等式;
(2)求出f(x)min=4,关于x的不等式f(x)≥|2a+1|不恒成立,可得|2a+1|>4,即可求实数a的取值范围.
解答 解:(1)x≤-1,|x+1|+|x-3|<6可化为-x-1-x+3<6,∴x>-2,∴-2<x≤-1.
-1<x<3,|x+1|+|x-3|<6可化为x+1-x+3<6,∴-2<x≤-1;
x≥3,|x+1|+|x-3|<6可化为x+1+x-3<6,∴x<4,∴-2<x≤-1,
综上所述,不等式的解集为{x|-2<x<4};
(2)∵f(x)=|x+1|+|x-3|≥|x+1-x+3|=4当且仅当-1≤x≤3时,等号成立,即f(x)min=4.
∵关于x的不等式f(x)≥|2a+1|不恒成立,
∴|2a+1|>4,∴a<-2.5或a>1.5.
点评 本题考查不等式的解法,考查不恒成立问题,考查学生的计算能力,属于中档题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
15.复数z=(a2-1)+(a-1)i(a∈R)为纯虚数,则z=( )
| A. | i | B. | -2i | C. | 2i | D. | -i |
12.“x<3”是“ln(x-2)<0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
19.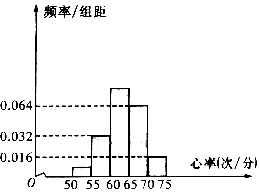 某学校的特长班有50名学生,其中有体育生20人,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60),…,第五组[70,75),按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为a:4:10.
某学校的特长班有50名学生,其中有体育生20人,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60),…,第五组[70,75),按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为a:4:10.
(1)求a的值,并求这50名学生心率的平均数;
(2)因为学习专业的原因,体育生常年进行系统的身体锻炼,艺术生则很少进行系统的身体锻炼,若从第一组和第二组的学生中随机抽取一名,该学生是体育生的概率为0.8,请将下面的列联表补充完整,并判断是否有99.5%的把握认为心率小于60次/分与常年进行系统的身体锻炼有关?请说明理由.
参考数据:
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
 某学校的特长班有50名学生,其中有体育生20人,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60),…,第五组[70,75),按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为a:4:10.
某学校的特长班有50名学生,其中有体育生20人,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60),…,第五组[70,75),按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为a:4:10.(1)求a的值,并求这50名学生心率的平均数;
(2)因为学习专业的原因,体育生常年进行系统的身体锻炼,艺术生则很少进行系统的身体锻炼,若从第一组和第二组的学生中随机抽取一名,该学生是体育生的概率为0.8,请将下面的列联表补充完整,并判断是否有99.5%的把握认为心率小于60次/分与常年进行系统的身体锻炼有关?请说明理由.
参考数据:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 心率小于60次/分 | 心率不小于60次/分 | 合计 | |
| 体育生 | 8 | 12 | 20 |
| 艺术生 | 2 | 28 | 30 |
| 合计 | 10 | 40 | 50 |
9.已知双曲线${C_1}:\frac{x^2}{6}-\frac{y^2}{2}=1$与双曲线${C_2}:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的离心率相同,且双曲线C2的左、右焦点分别为F1,F2,M是双曲线C2一条渐近线上的某一点,且OM⊥MF2,${S_{△OM{F_2}}}=8\sqrt{3}$,则双曲线C2的实轴长为( )
| A. | 4 | B. | $4\sqrt{3}$ | C. | 8 | D. | $8\sqrt{3}$ |
16.上世纪八十年代初,邓小平同志曾指出“在人才的问题上,要特别强调一下,必须打破常规去发现、选拔和培养杰出的人才”.据此,经省教育厅批准,某中学领导审时度势,果断作出于1985年开始施行超常实验班教学试验的决定.一时间,学生兴奋,教师欣喜,家长欢呼,社会热议.该中学实验班一路走来,可谓风光无限,硕果累累,尤其值得一提的是,1990年,全国共招收150名少年大学生,该中学就有19名实验班学生被录取,占全国的十分之一,轰动海内外.设该中学超常实验班学生第x年被录取少年大学生的人数为y.
(1)左下表为该中学连续5年实验班学生被录取少年大学生人数,求y关于x的线性回归方程,并估计第6年该中学超常实验班学生被录取少年大学生人数;
附1:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline y$-$\stackrel{∧}{b}$$\overline{x}$
(2)如表是从该校已经毕业的100名高中生录取少年大学生人数与是否接受超常实验班教育得到2×2列联表,完成上表,并回答:是否有95%以上的把握认为“录取少年大学生人数与是否接受超常实验班教育有关系”.
附2:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d.
(1)左下表为该中学连续5年实验班学生被录取少年大学生人数,求y关于x的线性回归方程,并估计第6年该中学超常实验班学生被录取少年大学生人数;
| 年份序号x | 1 | 2 | 3 | 4 | 5 |
| 录取人数y | 10 | 11 | 14 | 16 | 19 |
(2)如表是从该校已经毕业的100名高中生录取少年大学生人数与是否接受超常实验班教育得到2×2列联表,完成上表,并回答:是否有95%以上的把握认为“录取少年大学生人数与是否接受超常实验班教育有关系”.
附2:
| 接受超常实验班教育 | 未接受超常实验班教育 | 合计 | |
| 录取少年大学生 | 60 | 20 | 80 |
| 未录取少年大学生 | 10 | 10 | 20 |
| 合计 | 70 | 30 | 100 |
| P(k2≥k0) | 0.50 | 0.40 | 0.10 | 0.05 |
| k0 | 0.455 | 0.708 | 2.706 | 3.841 |