题目内容
9．从1，2，3，4四个数字中任取两个不同数字，则这两个数字之积小于5的概率为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{5}{6}$ |
分析 首先明确所有的事件数已经满足两个数字之积小于5的事件数，路古典概型的公式求概率．
解答 解：从1，2，3，4四个数字中任取两个不同数字共有${C}_{4}^{2}$=6种取法，
这两个数字之积小于5的事件有12，13，14共有3种，
由古典概型公式得从1，2，3，4四个数字中任取两个不同数字，
则这两个数字之积小于5的概率为到$\frac{3}{6}=\frac{1}{2}$；
故选B．
点评 本题考查了古典概型的概率求法；关键是明确所有事件以及满足条件的事件数．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
19．
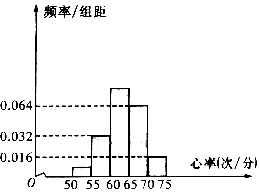某学校的特长班有50名学生，其中有体育生20人，艺术生30名，在学校组织的一次体检中，该班所有学生进行了心率测试，心率全部介于50次/分到75次/分之间，现将数据分成五组，第一组[50，55），第二组[55，60），…，第五组[70，75），按上述分组方法得到的频率分布直方图如图所示，已知图中从左到右的前三组的频率之比为a：4：10．
（1）求a的值，并求这50名学生心率的平均数；
（2）因为学习专业的原因，体育生常年进行系统的身体锻炼，艺术生则很少进行系统的身体锻炼，若从第一组和第二组的学生中随机抽取一名，该学生是体育生的概率为0.8，请将下面的列联表补充完整，并判断是否有99.5%的把握认为心率小于60次/分与常年进行系统的身体锻炼有关？请说明理由．
参考数据：
参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d
某学校的特长班有50名学生，其中有体育生20人，艺术生30名，在学校组织的一次体检中，该班所有学生进行了心率测试，心率全部介于50次/分到75次/分之间，现将数据分成五组，第一组[50，55），第二组[55，60），…，第五组[70，75），按上述分组方法得到的频率分布直方图如图所示，已知图中从左到右的前三组的频率之比为a：4：10．（1）求a的值，并求这50名学生心率的平均数；
（2）因为学习专业的原因，体育生常年进行系统的身体锻炼，艺术生则很少进行系统的身体锻炼，若从第一组和第二组的学生中随机抽取一名，该学生是体育生的概率为0.8，请将下面的列联表补充完整，并判断是否有99.5%的把握认为心率小于60次/分与常年进行系统的身体锻炼有关？请说明理由．
参考数据：
| P（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 心率小于60次/分 | 心率不小于60次/分 | 合计 | |
| 体育生 | 8 | 12 | 20 |
| 艺术生 | 2 | 28 | 30 |
| 合计 | 10 | 40 | 50 |
20．已知函数$f（x）=sin（{ωx+\frac{π}{6}}）（{0＜ω＜2}）$满足条件：$f（{-\frac{1}{2}}）=0$，为了得到y=f（x）的图象，可将函数g（x）=cosωx的图象向右平移m个单位（m＞0），则m的最小值为（ ）
| A． | 1 | B． | $\frac{1}{2}$ | C． | $\frac{π}{6}$ | D． | $\frac{π}{2}$ |
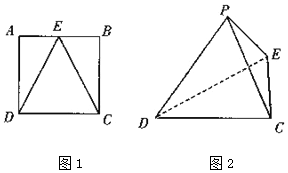如图1，2，E是正方形ABCD的AB边的中点，将△AED与△BEC分别沿ED、EC折起，使得点A与点B重合，记为点P，得到三棱锥P-CDE．