题目内容
直线x+y-2=0与两条坐标轴围成的三角形面积为 .
考点:三角形的面积公式
专题:解三角形
分析:令x=0,解得y=2;令y=0,解得x=2.即可得到:直线x+y-2=0与两条坐标轴围成的三角形面积S=
×2×2.
| 1 |
| 2 |
解答:
解:令x=0,解得y=2;令y=0,解得x=2.
∴直线x+y-2=0与两条坐标轴围成的三角形面积S=
×2×2=2.
故答案为:2.
∴直线x+y-2=0与两条坐标轴围成的三角形面积S=
| 1 |
| 2 |
故答案为:2.
点评:本题考查了直线与坐标轴的交点坐标和三角形的面积计算公式,属于基础题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
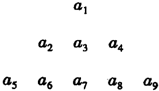 已知数列{an}的通项公式为an=2n(n∈N*),把数列{an}的各项排列成如图所示的三角形数阵:记M(s,t)表示该数阵中第s行的第t个数,则数阵中的偶数2010对应于( )
已知数列{an}的通项公式为an=2n(n∈N*),把数列{an}的各项排列成如图所示的三角形数阵:记M(s,t)表示该数阵中第s行的第t个数,则数阵中的偶数2010对应于( )| A、M(45,15) |
| B、M(45,25) |
| C、M(46,16) |
| D、M(46,25) |
a,b,c分别是△ABC的内角A,B,C的对边,下面能得出△ABC为锐角三角形的条件是( )
A、sinA+cosA=
| ||||
| B、tanA+tanB+tanC>0 | ||||
| C、b=3,c=3,B=30° | ||||
D、
|
一袋中装有5只球,编号为1,2,3,4,5,在袋中同时取3只,以ξ表示取出的三只球中的最小号码,则P(ξ=2)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
不等式(x2-4)(x-6)2≤0的解集为( )
| A、{x|-2≤x≤2} |
| B、{x|x≥2或x≤-2} |
| C、{x|-2≤x≤2或x=6} |
| D、{x|x≥2} |
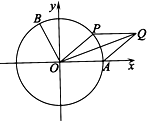 如图,以坐标原点O为圆心的单位圆与x轴正半轴相交于点A,点B,P在单位圆上,且
如图,以坐标原点O为圆心的单位圆与x轴正半轴相交于点A,点B,P在单位圆上,且