题目内容
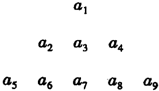 已知数列{an}的通项公式为an=2n(n∈N*),把数列{an}的各项排列成如图所示的三角形数阵:记M(s,t)表示该数阵中第s行的第t个数,则数阵中的偶数2010对应于( )
已知数列{an}的通项公式为an=2n(n∈N*),把数列{an}的各项排列成如图所示的三角形数阵:记M(s,t)表示该数阵中第s行的第t个数,则数阵中的偶数2010对应于( )| A、M(45,15) |
| B、M(45,25) |
| C、M(46,16) |
| D、M(46,25) |
考点:归纳推理
专题:等差数列与等比数列
分析:由图可得数阵中的前n行共有1+2+3+…+n=
项,进而可得偶数2010对应的位置.
| n(n+1) |
| 2 |
解答:
解:由数阵的排列规律知,数阵中的前n行共有1+2+3+…+n=
项,
当n=44时,共有990项,又数阵中的偶数2010是数列{an }的第1005项,
且
+15=1005,因此2010是数阵中第45行的第15个数,
数阵中的偶数2010对应于M(45,15)
故选A.
| n(n+1) |
| 2 |
当n=44时,共有990项,又数阵中的偶数2010是数列{an }的第1005项,
且
| 44×45 |
| 2 |
数阵中的偶数2010对应于M(45,15)
故选A.
点评:本题考查等差数列的通项公式和求和公式,要求熟练掌握等差数列的通项公式以及通项公式的应用.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
已知cosx=-
,且x∈[0,2π],则角x等于( )
| 1 |
| 2 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、-
|
下列函数中,在区间(0,+∞)上为增函数的是( )
A、y=-
| ||
| B、y=ln(x+2) | ||
| C、y=2-x | ||
D、y=x+
|
 以墙为一边,用篱笆围成长方形的场地,并用平行于一边的篱笆隔开(如图),
以墙为一边,用篱笆围成长方形的场地,并用平行于一边的篱笆隔开(如图),