题目内容
12.已知向量$\overrightarrow{a}$=(2,-4),$\overrightarrow{b}$=(-3,m),若|$\overrightarrow{a}$||$\overrightarrow{b}$|+$\overrightarrow{a}$•$\overrightarrow{b}$=0,则实数m=( )| A. | -6 | B. | 3 | C. | 6 | D. | 8 |
分析 根据条件即可求出$|\overrightarrow{a}||\overrightarrow{b}|=2\sqrt{5}•\sqrt{9+{m}^{2}}$,$\overrightarrow{a}•\overrightarrow{b}=-6-4m$,代入$|\overrightarrow{a}||\overrightarrow{b}|+\overrightarrow{a}•\overrightarrow{b}=0$即可得出关于m的方程,解出m即可.
解答 解:$|\overrightarrow{a}||\overrightarrow{b}|=2\sqrt{5}•\sqrt{9+{m}^{2}}$,$\overrightarrow{a}•\overrightarrow{b}=-6-4m$;
又$|\overrightarrow{a}||\overrightarrow{b}|+\overrightarrow{a}•\overrightarrow{b}=0$;
∴$2\sqrt{5}•\sqrt{9+{m}^{2}}-6-4m=0$;
∴$\sqrt{5}•\sqrt{9+{m}^{2}}=3+2m$,两边平方并整理得:
m2-12m+36=0;
解得m=6.
故选:C.
点评 考查根据向量坐标求向量长度的方法,向量数量积的坐标运算,无理方程的求法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.已知函数y=f(x)的反函数为y=f-1(x),则函数y=f(-x)与y=-f-1(x)的图象( )
| A. | 关于y轴对称 | B. | 关于原点对称 | ||
| C. | 关于直线x+y=0对称 | D. | 关于直线x-y=0对称 |
4.设a=1111111(2),b=2001(4),c=242(7),则a,b,c的大小关系是( )
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
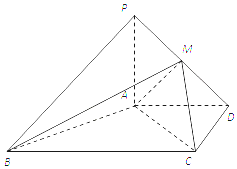 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2$\sqrt{2}$,BC=4$\sqrt{2}$,PA=2,点M在PD上.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2$\sqrt{2}$,BC=4$\sqrt{2}$,PA=2,点M在PD上.