题目内容
4.在平面直角坐标系xOy中,直线l1:kx-y+2=0与直线l2:x+ky-2=0相交于点P,则当实数k变化时,点P到直线x-y-4=0的距离的最大值为3$\sqrt{2}$.分析 直线l1:kx-y+2=0与直线l2:x+ky-2=0的斜率乘积=k×$(-\frac{1}{k})$=-1,(k=0时,两条直线也相互垂直),并且两条直线分别经过定点:M(0,2),N(2,0).可得点M到直线x-y-4=0的距离d为最大值.
解答 解:∵直线l1:kx-y+2=0与直线l2:x+ky-2=0的斜率乘积=k×$(-\frac{1}{k})$=-1,(k=0时,两条直线也相互垂直),并且两条直线分别经过定点:M(0,2),N(2,0).
∴两条直线的交点在以MN为直径的圆上.并且kMN=-1,可得MN与直线x-y-4=0垂直.
∴点M到直线x-y-4=0的距离d=$\frac{|0-2-4|}{\sqrt{2}}$=3$\sqrt{2}$为最大值.
故答案为:3$\sqrt{2}$.
点评 本题考查了直线的方程、圆的性质、相互垂直的直线斜率之间的关系、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.已知向量$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(0,1),则下列向量中与向量2$\overrightarrow{a}$+$\overrightarrow{b}$垂直的是( )
| A. | $\overrightarrow{a}$+$\overrightarrow{b}$ | B. | $\overrightarrow{a}$-$\overrightarrow{b}$ | C. | 2$\overrightarrow{a}$-$\overrightarrow{b}$ | D. | $\overrightarrow{a}$-2$\overrightarrow{b}$ |
15.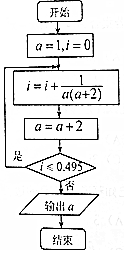 已知某程序框图如图所示,则执行该程序后输出的结果是( )
已知某程序框图如图所示,则执行该程序后输出的结果是( )
 已知某程序框图如图所示,则执行该程序后输出的结果是( )
已知某程序框图如图所示,则执行该程序后输出的结果是( )| A. | 98 | B. | 99 | C. | 100 | D. | 101 |
16.如图,程序输出的结果s=1320,则判断框中应填( )


| A. | i≥10? | B. | i<10? | C. | i≥11? | D. | i<11? |
 如图,在平面直角坐标系xOy中,焦点在x轴上的椭圆C:$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{{b}^{2}}$=1经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).
如图,在平面直角坐标系xOy中,焦点在x轴上的椭圆C:$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{{b}^{2}}$=1经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).