题目内容
1.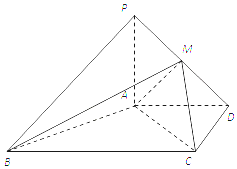 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2$\sqrt{2}$,BC=4$\sqrt{2}$,PA=2,点M在PD上.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2$\sqrt{2}$,BC=4$\sqrt{2}$,PA=2,点M在PD上.(Ⅰ)求证:AB⊥PC;
(Ⅱ)若BM与平面ABCD所成角的正切值为$\frac{{\sqrt{26}}}{26}$,求四棱锥M-ABCD的体积.
分析 (Ⅰ)设E为BC的中点,连结AE,求解三角形可得AB⊥AC,又PA⊥平面ABCD,得AB⊥PA,再由线面垂直的判定可得AB⊥面PAC,故有AB⊥PC;
(Ⅱ)结合(Ⅰ)可得∠BAD=135°,过M作MG⊥AD于G,设AG=x,则GD=$2\sqrt{2}-x$,有MG=$\frac{4-\sqrt{2}x}{2}$.在△ABG中,由余弦定理可得BG,由BM与平面ABCD所成角的正切值为$\frac{\sqrt{26}}{26}$,得M为PD的中点,再由棱锥体积公式求得四棱锥M-ABCD的体积.
解答 解:(Ⅰ)证明:如图,设E为BC的中点,连结AE,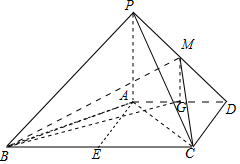
则AD=EC,又AD∥EC,∴四边形AECD为平行四边形,
故AE⊥BC,又AE=BE=EC=$2\sqrt{2}$,
∴∠ABC=∠ACB=45°,故AB⊥AC,
又∵PA⊥平面ABCD,∴AB⊥PA,
∵PA∩AC=A,∴AB⊥平面PAC,故有AB⊥PC;
(Ⅱ)由(1)知AB⊥AC,可得∠BAD=135°,
过M作MG⊥AD于G,设AG=x,则GD=$2\sqrt{2}-x$,∴MG=$\frac{4-\sqrt{2}x}{2}$.
在△ABG中,由余弦定理可得:BG=$\sqrt{{4}^{2}+{x}^{2}+4\sqrt{2}x}$,
由BM与平面ABCD所成角的正切值为$\frac{\sqrt{26}}{26}$,得$\frac{\frac{4-\sqrt{2}x}{2}}{\sqrt{16+{x}^{2}+4\sqrt{2}x}}=\frac{\sqrt{26}}{26}$,解得x=$\sqrt{2}$,
∴MG=1,即M为PD的中点.
此时四棱锥M-ABCD的体积为$\frac{1}{3}×\frac{1}{2}(2\sqrt{2}+4\sqrt{2})×2\sqrt{2}×1$=4.
点评 本题考查直线与平面垂直的判定和性质,考查空间想象能力和思维能力,考查多面体体积的求法,是中档题.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案| A. | $(1,\sqrt{10})$ | B. | $(\sqrt{10},+∞)$ | C. | $({1,\sqrt{10}}]$ | D. | $[{\sqrt{10}}\right.,+∞)$ |
| A. | -1 | B. | $\frac{4}{5}$ | C. | -i | D. | $\frac{4}{5}i$ |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |