题目内容
2.2017年1月25日智能共享单车项目摩拜单车正式登陆济南,两种车型采用分段计费的方式,Mobike Lite型(Lite版)和经典版每30分钟收0.5元(不足30分钟的部分按30分钟计算).有甲、乙、丙三人相互对立的到租车点租车骑行(各租一车一次).设甲、乙、丙不超过30分钟还车的概率分别为$\frac{3}{4}$,$\frac{2}{3}$,$\frac{1}{2}$,三人租车时间都不会超过60分钟,甲、乙均租用Lite版单车,丙租用经典版单车.(1)求甲、乙两人所付的费用之和等于丙所付的费用的概率;
(2)设甲、乙、丙三人所付费用之和为随机变量ξ,求ξ的分布列和数学期望.
分析 (1)甲、乙两人所付的费用之和等于丙所付的费用必然是:甲、乙两人半小时内还车,而丙超过30分钟还车.其概率P=$\frac{3}{4}×\frac{2}{3}$×$(1-\frac{1}{2})$.
(2)ξ的取值可能为1.5,2,2.5,3.利用相互独立与互斥事件的概率计算公式即可得出.
解答 解:(1)甲、乙两人所付的费用之和等于丙所付的费用必然是:甲、乙两人半小时内还车,而丙超过30分钟还车.其概率P=$\frac{3}{4}×\frac{2}{3}$×$(1-\frac{1}{2})$=$\frac{1}{4}$.
(2)ξ的取值可能为1.5,2,2.5,3.
P(ξ=1.5)=$\frac{3}{4}$×$\frac{2}{3}$×$\frac{1}{2}$=$\frac{1}{4}$,P(ξ=2)=(1-$\frac{3}{4}$)×$\frac{2}{3}$×$\frac{1}{2}$+$\frac{3}{4}$×(1-$\frac{2}{3}$)×$\frac{1}{2}$+$\frac{3}{4}$×$\frac{2}{3}$×(1-$\frac{1}{2}$)=$\frac{11}{24}$,
P(ξ=2.5)=(1-$\frac{3}{4}$)×(1-$\frac{2}{3}$)×$\frac{1}{2}$+$\frac{3}{4}$×(1-$\frac{2}{3}$)×(1-$\frac{1}{2}$)+(1-$\frac{3}{4}$)×$\frac{2}{3}$×(1-$\frac{1}{2}$)=$\frac{6}{24}$,
P(ξ=3)=(1-$\frac{3}{4}$)×(1-$\frac{2}{3}$)×(1-$\frac{1}{2}$)=$\frac{1}{24}$.
∴ξ的分布列为:
| ξ | 1.5 | 2 | 2.5 | 3 |
| P | $\frac{1}{4}$ | $\frac{11}{24}$ | $\frac{6}{24}$ | $\frac{1}{24}$ |
点评 本题考查了相互独立与互斥事件的概率计算公式、随机变量的分布列的概率数学期望,考查了推理能力与计算能力,属于中档题.

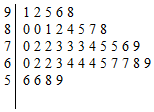 中国诗词大会的播出引发了全民的读书热,某小学语文老师在班里开展了一次诗词默写比赛,班里40名学生得分数据的茎叶图如图所示.若规定得分不小于85分的学生得到“诗词达人”的称号,小于85分且不小于70分的学生得到“诗词能手”的称号,其他学生得到“诗词爱好者”的称号,根据该次比赛的成就按照称号的不同进行分层抽样抽选10名学生,则抽选的学生中获得“诗词能手”称号的人数为( )
中国诗词大会的播出引发了全民的读书热,某小学语文老师在班里开展了一次诗词默写比赛,班里40名学生得分数据的茎叶图如图所示.若规定得分不小于85分的学生得到“诗词达人”的称号,小于85分且不小于70分的学生得到“诗词能手”的称号,其他学生得到“诗词爱好者”的称号,根据该次比赛的成就按照称号的不同进行分层抽样抽选10名学生,则抽选的学生中获得“诗词能手”称号的人数为( )