题目内容
5.设实数x,y满足约束条件$\left\{\begin{array}{l}{x+y≥0}\\{x-y≤0}\\{x+3y≤3}\end{array}\right.$,则$\frac{x+y}{\sqrt{{x}^{2}+{y}^{2}}}$的取值范围是[0,2].分析 画出约束条件的可行域,化简目标函数,转化为直线的斜率问题,通过函数的值域求解目标函数的范围即可.
解答  解:约束条件的可行域如图:由$\left\{\begin{array}{l}{x+y=0}\\{x+3y=3}\end{array}\right.$可得A(-$\frac{3}{2}$,$\frac{3}{2}$),
解:约束条件的可行域如图:由$\left\{\begin{array}{l}{x+y=0}\\{x+3y=3}\end{array}\right.$可得A(-$\frac{3}{2}$,$\frac{3}{2}$),
$\left\{\begin{array}{l}{x-y=0}\\{x+3y=3}\end{array}\right.$可得B($\frac{3}{4}$,$\frac{3}{4}$),
则$\frac{x+y}{\sqrt{{x}^{2}+{y}^{2}}}$=$\sqrt{1+\frac{2xy}{{x}^{2}+{y}^{2}}}$=$\sqrt{1+\frac{2}{\frac{y}{x}+\frac{x}{y}}}$,由题意可得$\frac{y}{x}$∈[-1,1],令t=$\frac{y}{x}$∈[-1,1],则$\frac{y}{x}+\frac{x}{y}$=t+$\frac{1}{t}$∈[2,+∞)∪(-∞,-2],
∴$\sqrt{1+\frac{2}{\frac{y}{x}+\frac{x}{y}}}$∈[0,2].
故答案为:[0,2].
点评 本题考查线性规划的简单应用,考查数形结合以及函数的最值的求法,考查转化思想以及计算能力.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
15.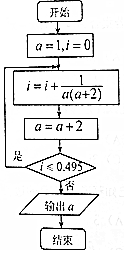 已知某程序框图如图所示,则执行该程序后输出的结果是( )
已知某程序框图如图所示,则执行该程序后输出的结果是( )
 已知某程序框图如图所示,则执行该程序后输出的结果是( )
已知某程序框图如图所示,则执行该程序后输出的结果是( )| A. | 98 | B. | 99 | C. | 100 | D. | 101 |
16.如图,程序输出的结果s=1320,则判断框中应填( )


| A. | i≥10? | B. | i<10? | C. | i≥11? | D. | i<11? |
13.已知z1=1-3i,z2=3+i,其中i是虚数单位,则$\frac{{\overline{z_1}}}{z_2}$的虚部为( )
| A. | -1 | B. | $\frac{4}{5}$ | C. | -i | D. | $\frac{4}{5}i$ |
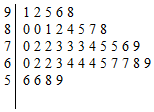 中国诗词大会的播出引发了全民的读书热,某小学语文老师在班里开展了一次诗词默写比赛,班里40名学生得分数据的茎叶图如图所示.若规定得分不小于85分的学生得到“诗词达人”的称号,小于85分且不小于70分的学生得到“诗词能手”的称号,其他学生得到“诗词爱好者”的称号,根据该次比赛的成就按照称号的不同进行分层抽样抽选10名学生,则抽选的学生中获得“诗词能手”称号的人数为( )
中国诗词大会的播出引发了全民的读书热,某小学语文老师在班里开展了一次诗词默写比赛,班里40名学生得分数据的茎叶图如图所示.若规定得分不小于85分的学生得到“诗词达人”的称号,小于85分且不小于70分的学生得到“诗词能手”的称号,其他学生得到“诗词爱好者”的称号,根据该次比赛的成就按照称号的不同进行分层抽样抽选10名学生,则抽选的学生中获得“诗词能手”称号的人数为( )