题目内容
18.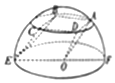 如图所示,三棱柱OAD-EBC,其中A,C,B,D,E均为以O为球心,半径为4的半球面上,EF为直径,侧面ABCD为边长等于4的正方形,则三棱柱OAD-EBC的高为( )
如图所示,三棱柱OAD-EBC,其中A,C,B,D,E均为以O为球心,半径为4的半球面上,EF为直径,侧面ABCD为边长等于4的正方形,则三棱柱OAD-EBC的高为( )| A. | $\frac{8\sqrt{6}}{3}$ | B. | $\frac{4\sqrt{6}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
分析 连结OB,OC,判断O-ABCD的形状,求出VO-ABD,利用三棱锥的体积公式建立方程,求出结果.
解答 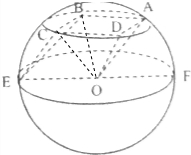 解:连结OB,OC,由题意可知O-ABCD是棱长为4的四棱锥,O到底面ABCD的距离为h=$\sqrt{{4}^{2}-(2\sqrt{2})^{2}}$=2$\sqrt{2}$.O到AD的距离为$\sqrt{8+4}$=2$\sqrt{3}$
解:连结OB,OC,由题意可知O-ABCD是棱长为4的四棱锥,O到底面ABCD的距离为h=$\sqrt{{4}^{2}-(2\sqrt{2})^{2}}$=2$\sqrt{2}$.O到AD的距离为$\sqrt{8+4}$=2$\sqrt{3}$
VO-ABD=$\frac{1}{3}$S△ABD•h=$\frac{1}{3}$×$\frac{1}{2}$×4×4×2$\sqrt{2}$=$\frac{16\sqrt{2}}{3}$.
三棱柱OAD-EBC的高为h′,则$\frac{1}{3}×\frac{1}{2}×4×2\sqrt{3}×h′$=$\frac{16\sqrt{2}}{3}$,
∴h′=$\frac{4\sqrt{6}}{3}$.
故选:B.
点评 本题考查球与内接几何体的关系,三棱锥的体积的求法以及关系的应用,考查转化思想.

练习册系列答案
相关题目
6.已知P为抛物线y2=4x上任意一点,抛物线的焦点为F,点A(2,1)是平面内一点,则|PA|+|PF|的最小值为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
13.已知f(x)=$\left\{\begin{array}{l}{e^x}+ax,x>0\\ \frac{1}{e^x}-ax,x<0\end{array}$,若函数f(x)有四个零点,则实数a的取值范围是( )
| A. | $({-∞,-\frac{1}{e}})$ | B. | (-∞,-e) | C. | (e,+∞) | D. | $({\frac{1}{e},+∞})$ |
10.设Sn为等比数列{an}的前n项和,若8a2+a5=0,则$\frac{{S}_{5}}{{S}_{2}}$等于( )
| A. | $\frac{11}{3}$ | B. | 5 | C. | -8 | D. | -11 |
7.抛物线y=4x2的焦点到准线的距离为( )
| A. | 2 | B. | $\frac{1}{8}$ | C. | 4 | D. | $\frac{1}{4}$ |
8.从1,2,…,9这九个数中,随机抽取3个不同的数,则这3个数的和为奇数的概率是( )
| A. | $\frac{5}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{11}{21}$ | D. | $\frac{10}{21}$ |