题目内容
已知f（x）是奇函数，当x＜0时，f（x）=x3+x2，则f（2）= ．
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：本题利用函数f（x）是奇函数，将f（2）转化为求f（-2），再用当x＜0时，f（x）=x3+x2，求出f（-2）的值，从而得到本题结论．
解答：
解：∵函数f（x）是奇函数，
∴f（-x）=f（x）．
∴f（2）=-f（-2）．
∵当x＜0时，f（x）=x3+x2，
∴f（-2）=（-2）3+（-2）2=-4．
∴f（2）=4．
故答案为4．
∴f（-x）=f（x）．
∴f（2）=-f（-2）．
∵当x＜0时，f（x）=x3+x2，
∴f（-2）=（-2）3+（-2）2=-4．
∴f（2）=4．
故答案为4．
点评：本题考查了用函数的奇偶性求函数的值，本题难度不大，属于基础题．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
已知集合D={x|
＞0}，若a，b∈D且
+
=
，则9a•3b的最小值为（ ）
| 24-x |
| x-9 |
| 1 |
| a |
| 1 |
| 2b |
| 1 |
| 12 |
| A、27 |
| B、327 |
| C、54 |
| D、354 |
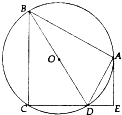如图，⊙O是四边形ABCD的外接圆，BD是⊙O的直径，AE⊥CD于点E，∠BDA=∠EDA．
求曲线y=sinx，y=cosx与直线x=0，x=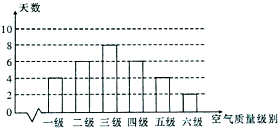
根据空气质量指数AQJ（为整数）的不同，可将空气质量分级如下表：执行如图所示的程序框图，则输出结果S的值为（ ）
A、
| ||
| B、0 | ||
C、-
| ||
| D、-1 |