题目内容
 根据空气质量指数AQJ(为整数)的不同,可将空气质量分级如下表:
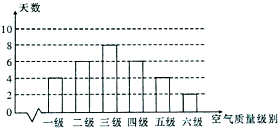
根据空气质量指数AQJ(为整数)的不同,可将空气质量分级如下表:某市2014年11月1日-11月30日,对空气质量指数AQI进行监测,获得数据后得到如条形图:
(1)市教育局规定在空气质量类别达到中度污染及以上时学生不宜进行户外跑步活动,估计该城市本月(按30天计)学生可以进行户外跑步活动的概率;
(2)在上述30个监测数据中任取2个,设ξ为空气质量类别颜色为绿色的天数,求ξ的分布列与数学期望.
| AQI(数值) | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 空气质量类别颜色 | 绿色 | 黄色 | 橙色 | 红色 | 紫色 | 褐红色 |
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:概率与统计
分析:(1)由条形统计图知空气质量类别达到中度污染及以上的天数为12天,由此利用对立事件概率计算公式能求出该城市本月学生可以进行户外跑步活动的概率.
(2)由已知得ξ的可能可值为0,1,2,分别求出相应的概率,由此能求出ξ的分布列与数学期望.
(2)由已知得ξ的可能可值为0,1,2,分别求出相应的概率,由此能求出ξ的分布列与数学期望.
解答:
解:(1)由条形统计图知:
空气质量类别达到中度污染及以上的天数为:
6+4+2=12天,
∴该城市本月学生可以进行户外跑步活动的概率P=1-
=
.
(2)由已知得ξ的可能可值为0,1,2,
P(ξ=0)=
=
,
P(ξ=1)=
=
,
P(ξ=2)=
=
,
∴ξ的分布列为:
∴Eξ=0×
+1×
+2×
=
.
空气质量类别达到中度污染及以上的天数为:
6+4+2=12天,
∴该城市本月学生可以进行户外跑步活动的概率P=1-
| 12 |
| 30 |
| 3 |
| 5 |
(2)由已知得ξ的可能可值为0,1,2,
P(ξ=0)=
| ||
|
| 65 |
| 84 |
P(ξ=1)=
| ||||
|
| 104 |
| 435 |
P(ξ=2)=
| ||
|
| 2 |
| 145 |
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 65 |
| 87 |
| 104 |
| 435 |
| 2 |
| 145 |
| 116 |
| 435 |
点评:本题考查概率的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
