题目内容
在△ABC中,a,b,c分别是角A、B、C的对边,若a=1,且2cosC+c=2b,则△ABC的周长的取值范围是( )
| A、(1,3] |
| B、[2,4] |
| C、(2,3] |
| D、[3,5] |
考点:余弦定理
专题:三角函数的求值
分析:由余弦定理求得 cosC,代入已知等式可得(b+c)2-1=3bc,利用基本不等式求得 b+c≤2,故a+b+c≤3.再由三角形任意两边之和大于第三边求得a+b+c>2,由此求得△ABC的周长的取值范围.
解答:
解:△ABC中,由余弦定理可得:2cosC=
,
∵a=1,2cosC+c=2b,
∴
+c=2b,化简可得:(b+c)2-1=3bc,
∵bc≤(
)2,
∴(b+c)2-1≤3×(
)2,
解得:b+c≤2(当且仅当b=c时,取等号).
∴a+b+c≤3,
再由任意两边之和大于第三边可得:b+c>a=1,
故有a+b+c>2,
则△ABC的周长的取值范围是(2,3],
故选:C.
| a2+b2-c2 |
| 2ab |
∵a=1,2cosC+c=2b,
∴
| 1+b2-c2 |
| b |
∵bc≤(
| b+c |
| 2 |
∴(b+c)2-1≤3×(
| b+c |
| 2 |
解得:b+c≤2(当且仅当b=c时,取等号).
∴a+b+c≤3,
再由任意两边之和大于第三边可得:b+c>a=1,
故有a+b+c>2,
则△ABC的周长的取值范围是(2,3],
故选:C.
点评:此题考查了余弦定理,以及基本不等式的运用,熟练掌握余弦定理是解本题的关键.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
若角α的终边上有一点P(a,a),a∈R且a≠0,则sinα的值是( )
A、
| ||||
B、-
| ||||
C、±
| ||||
| D、1 |
已知点F(-c,0)(c>0)是双曲线
-
=1的左焦点,离心率为e,过F且平行于双曲线渐近线的直线与圆x2+y2=c2交于点P,且点P在抛物线y2=3cx上,则e2=( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如果θ=3rad,那么角θ的终边所在的象限是( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
如图,已知
=
,则( )

| AB |
| 1 |
| 3 |
| AP |

A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
命题“?x>0,sinx=0”的否定为( )
| A、?x>0,sinx≠0 |
| B、?x≤0,sinx≠0 |
| C、?x≤0,sinx≠0 |
| D、?x>0,sinx≠0 |
点P(x,y)在直线x+y-2=0上,则P到原点距离的最小值是( )
A、2
| ||
B、
| ||
| C、1 | ||
| D、2. |
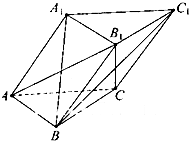 已知三棱柱ABC-A1B1C1中,底面边长和侧棱长均为a,侧面A1ACC1⊥底面ABC,A1B=
已知三棱柱ABC-A1B1C1中,底面边长和侧棱长均为a,侧面A1ACC1⊥底面ABC,A1B=