题目内容
已知点F(-c,0)(c>0)是双曲线
-
=1的左焦点,离心率为e,过F且平行于双曲线渐近线的直线与圆x2+y2=c2交于点P,且点P在抛物线y2=3cx上,则e2=( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:利用抛物线的性质、双曲线的渐近线、直线平行的性质、圆的性质、相似三角形的性质即可得出.
解答:
解:如图,设抛物线y2=3cx的准线为l,作PQ⊥l于Q,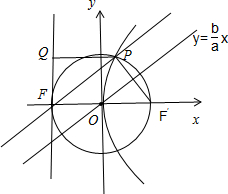
设双曲线的右焦点为F′,P(x,y).
由题意可知FF′为圆x2+y2=c2的直径,
∴PF′⊥PF,且tan∠PFF′=
,|FF′|=2C,
满足
将①代入②得x2+3cx-c2=0,
解得,x=
,
即,x=
c,负值舍去)
代入第三个方程
=
,即y=
•
再将y代入①得,
=
=e2-1
化简得,e=
.
故选:D.

设双曲线的右焦点为F′,P(x,y).
由题意可知FF′为圆x2+y2=c2的直径,
∴PF′⊥PF,且tan∠PFF′=
| b |
| a |
满足
|
将①代入②得x2+3cx-c2=0,
解得,x=
-3c±
| ||
| 2 |
即,x=
| ||
| 2 |
代入第三个方程
| y |
| x+c |
| b |
| a |
| bc |
| a |
| ||
| 2 |
再将y代入①得,
| b2 |
| a2 |
6(
| ||
(
|
化简得,e=
| ||
| 3 |
故选:D.
点评:本题考查双曲线的性质,掌握抛物线的性质、双曲线的渐近线、直线平行的性质、圆的性质是解题的关键.

练习册系列答案
相关题目
给出命题p:f(x)=sinx+
cosx的周期为π;命题q:若数列{an}前n项和Sn=n2+2n,则数列{an}为等差数列,则下列四个命题“p且q”,“p或q”,“非p”,“非q”中,真命题个数为( )
| 3 |
| A、0个 | B、1个 | C、2个 | D、3个 |
二维空间中,圆的一维测度(周长)l=2πr,二维测度(面积)S=πr2;三维空间中,球的二维测度(表面积)S=4πr2,三维测度(体积)V=
πr3.应用合情推理,若四维空间中,“超球”的三维测度V=8πr3,则其四维测度W=( )
| 4 |
| 3 |
| A、2πr4 |
| B、3πr4 |
| C、4πr4 |
| D、6πr4 |
用反证法证明“若△ABC的三边长a,b,c的倒数成等差数列,则B<
”时,“假设”应为( )
| π |
| 2 |
A、B<
| ||
B、B>
| ||
C、B≤
| ||
D、B≥
|
极坐标方程4sin2θ=3表示曲线是 ( )
| A、两条射线 | B、抛物线 |
| C、圆 | D、两条相交直线 |
椭圆
+
=1上一点满足∠F1PF2=60°(F1,F2为焦点),则△F1PF2的面积为( )
| y2 |
| 25 |
| x2 |
| 9 |
| A、3 | ||||
B、3
| ||||
C、
| ||||
D、6
|
函数y=x3与x轴,直线x=1围成的封闭图形的面积为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,a,b,c分别是角A、B、C的对边,若a=1,且2cosC+c=2b,则△ABC的周长的取值范围是( )
| A、(1,3] |
| B、[2,4] |
| C、(2,3] |
| D、[3,5] |