题目内容
19.在△ABC中,内角A,B,C的对边分别是a,b,c,向量$\overrightarrow m=({\frac{a}{2},\frac{c}{2}}),\overrightarrow n=({cosC,cosA})$,且$\overrightarrow n•\overrightarrow m=bcosB$.(1)求B的值;
(2)若$cos\frac{A-C}{2}=\sqrt{3}sinA$,且$|{\overrightarrow m}|=\sqrt{5}$,求△ABC的面积.
分析 (1)由$\overrightarrow{n}•\overrightarrow{m}=bcosB$进行数量积的坐标运算,并由正弦定理即可求出$cosB=\frac{1}{2}$,从而得到$B=\frac{π}{3}$;
(2)可得到C=$\frac{2π}{3}-A$,从而由$cos\frac{A-C}{2}=\sqrt{3}sinA$求出tanA=$\frac{\sqrt{3}}{3}$,进而得出C=$\frac{π}{2}$,从而有c=2a①,并且根据条件有a2+c2=20②,这样联立①②即可求出a,c,进而求出b的值,从而可求出△ABC的面积.
解答 解:(1)$\overrightarrow{n}•\overrightarrow{m}=bcosB$;
∴$\frac{a}{2}cosC+\frac{c}{2}cosA=bcosB$;
∴sinAcosC+cosAsinC=2sinBcosB;
∴sin(A+C)=2sinBcosB;
即sinB=2sinBcosB;
∵0<B<π;
∴sinB≠0;
∴$cosB=\frac{1}{2}$;
∴$B=\frac{π}{3}$;
(2)C=π-A-B=$\frac{2π}{3}-A$;
由$cos\frac{A-C}{2}=\sqrt{3}sinA$得,$cos(A-\frac{π}{3})=\sqrt{3}sinA$;
∴$\frac{1}{2}cosA+\frac{\sqrt{3}}{2}sinA=\sqrt{3}sinA$;
∴$cosA=\sqrt{3}sinA$;
∴$tanA=\frac{\sqrt{3}}{3}$;
∵$0<A<\frac{2π}{3}$;
∴$A=\frac{π}{6}$;
∴$C=\frac{π}{2}$;
在Rt△ABC中,$a=\frac{1}{2}c$,即c=2a;
又$|\overrightarrow{m}|=\sqrt{5}$;
即$\frac{{a}^{2}+{c}^{2}}{4}=5$;
∴5a2=20;
∴a=2,c=4;
∴$b=2\sqrt{3}$;
∴${S}_{△ABC}=\frac{1}{2}×2×2\sqrt{3}=2\sqrt{3}$.
点评 考查数量积的坐标运算,正弦定理,两角和差的正余弦公式,以及已知三角函数值求角.

 小学教材完全解读系列答案
小学教材完全解读系列答案| A. | 2 | B. | -2 | C. | $-2+\sqrt{5}$ | D. | $-2-\sqrt{5}$ |
| A. | $\frac{1}{12}$ | B. | $\frac{1}{6}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{3}$ |
| A. | “am2<bm2”是“a<b”成立的充分不必要条件 | |
| B. | 命题“?x∈R,x3-x2-1≤0”的否定是“?x0∈R,x03-x02-1>0” | |
| C. | “若a=1,则直线x+y=0和直线x-ay=0互相垂直”的逆否命题为真命题 | |
| D. | 若p∧q为假命题,则p,q均为假命题 |
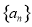 的前
的前 项和为
项和为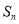 ,且
,且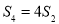 ,
,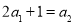 .
.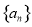 的通项公式;
的通项公式;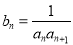 ,求
,求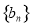 的前
的前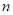 项和
项和 .
.