Question

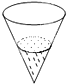如图，一个倒立的圆锥，底面半径为10cm，高为15cm，先将一定量的水注入其中，其形成的圆锥高为hcm，底面半径为rcm
（1）求水的体积；
（2）若形成的圆锥的体积恰为原来圆锥体积的一半，求h的值（精确到0.01）

Answer 1

考点：旋转体（圆柱、圆锥、圆台）

专题：空间位置关系与距离

分析：（1）由已知中注入形成的圆锥高为hcm，底面半径为rcm代入圆锥体积公式，可得水的体积；
（2）由注水形成的圆锥与原来的圆锥相似，可得r=

2

3

h，结合形成的圆锥的体积恰为原来圆锥体积的一半，根据等积法，构造关于h的方程，解方程可得答案．

解答： 解：（1）∵注入形成的圆锥高为hcm，底面半径为rcm
故水的体积V_水=

1

3

πr2hcm³，
（2）由于注水形成的圆锥与原来的圆锥相似，
故h：r=15：10，
即r=

2

3

h，
形成的圆锥的体积恰为原来圆锥体积的一半，
则

1

3

πr2h=

4

27

πh3=

1

2

×

1

3

π102×15，
解得h=

15

2

3	4

≈11.85cm

点评：本题考查的知识点是圆锥的体积，难度不大，但计算不太方便．