题目内容
已知{an}是等差数列，且a2+a3+a8+a11=48，a5+a7= ．
考点：等差数列的前n项和
专题：集合
分析：由已知得4a1+20d=48，由此能求出a5+a7=2a1+10d=24．
解答：
解：∵{an}是等差数列，且a2+a3+a8+a11=48，
∴4a1+20d=48，
∴a5+a7=2a1+10d=24．
故答案为：24．
∴4a1+20d=48，
∴a5+a7=2a1+10d=24．
故答案为：24．
点评：本题考查等差数列中两项和的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
若函数y=
的定义域为R，则k的取值范围是（ ）
| kx2-6kx+(k+8) |
| A、[1，+∞） |
| B、（1，+∞） |
| C、{0}∪（1，+∞） |
| D、[0，1] |
若△ABC的三个内角满足sinA：sinB：sinC=1：2：
，则△ABC（ ）
| 6 |
| A、一定是锐角三角形 |
| B、一定是直角三角形 |
| C、一定是钝角三角形 |
| D、可能是钝角三角形 |
设a＞0，b＞0，A（1，-2），B（a，-1），C（-b，0），若A、B、C三点共线，则
+
的最小值是（ ）
| 1 |
| a |
| 1 |
| b |
A、3+2
| ||
B、4
| ||
| C、6 | ||
D、
|
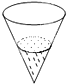如图，一个倒立的圆锥，底面半径为10cm，高为15cm，先将一定量的水注入其中，其形成的圆锥高为hcm，底面半径为rcm