题目内容
命题“对任意{x|-1≤x≤1}，都有2x2+4x-7≠0”的否定是（ ）
| A、对任意x∈R，都有λ=3 |
| B、不存在x∈R，使得x2＜1 |
| C、存在x0∈R，使得x02≥1 |
| D、存在x∈R，使得2x2+4x-7=0 |
考点：命题的否定
专题：简易逻辑
分析：直接利用全称命题的否定是特称命题写出结果即可．
解答：
解：因为全称命题的否定是特称命题，所以命题“对任意{x|-1≤x≤1}，都有2x2+4x-7≠0”的否定是：存在x∈R，使得2x2+4x-7=0．
故选：D．
故选：D．
点评：本题考查命题的否定，全称命题与特称命题的否定关系，基本知识的考查．
练习册系列答案
字词句段篇系列答案
相关题目
设a＞0，b＞0，A（1，-2），B（a，-1），C（-b，0），若A、B、C三点共线，则
+
的最小值是（ ）
| 1 |
| a |
| 1 |
| b |
A、3+2
| ||
B、4
| ||
| C、6 | ||
D、
|
已知集合A={-1，2}，B={x|mx+1=0}，若A∩B=B，则所有实数m的值组成的集合是（ ）
| A、{-1，2} | ||
B、{1，-
| ||
C、{1，0，-
| ||
D、{-1，0，
|
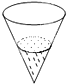如图，一个倒立的圆锥，底面半径为10cm，高为15cm，先将一定量的水注入其中，其形成的圆锥高为hcm，底面半径为rcm