题目内容
设各项均为正数的数列{an}的前n项和为Sn,满足
=4Sn+4n+1,n∈N*且a2,a5,a14恰好是等比数列{bn}的前三项.
(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)记数列{bn}的前n项和为Tn,若对任意的n∈N*,(T n+
)k≥3n-6恒成立,求实数k的取值范围.
| a | 2 n+1 |
(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)记数列{bn}的前n项和为Tn,若对任意的n∈N*,(T n+
| 3 |
| 2 |
考点:数列与不等式的综合,数列的求和,数列递推式
专题:等差数列与等比数列
分析:(Ⅰ)由4Sn=an+12-4n-1得,当n≥2时,4Sn-1=an2-4(n-1)-1,两式相减并化简,得数列{an}为等差数列,再由题目中其他条件计算出{an}、{bn}的通项公式.
(Ⅱ)由(Ⅰ)计算得到Tn=
,再进行参数分离,将题中不等式转化为:k≥
对n∈N*恒成立,令cn=
,作差确定数列的单调性,求出数列的最小值即可.
(Ⅱ)由(Ⅰ)计算得到Tn=
| 3n+1-3 |
| 2 |
| 2n-4 |
| 3n |
| 2n-4 |
| 3n |
解答:
(Ⅰ)由题意,4Sn=an+12-4n-1,
当n≥2时,4Sn-1=an2-4(n-1)-1,
∴4an=4Sn-4Sn-1=an+12-an2-4,
an+12=an2+4an+4=(an+2)2,
又an>0,∴an+1=an+2.
∴当n≥2时,{an}是公差d=2的等差数列.
又a2,a5,a14构成等比数列,a52=a2•a14,
(a2+6)2=a2•(a2+24),解得a2=3,
由条件可知,4a1=a22-5=4,∴a1=1,
又a2-a1=3-1=2,∴{an}是首项a1=1,公差d=2的等差数列.数列{an} 的通项公式为an=2n-1,
则b1=a2=3,b2=a5=9,b3=a14=27,且{bn}是等比数列,
∴数列{bn}的通项公式为bn=3n.
(Ⅱ)Tn=
=
=
,
∴(
+
)k≥3n-6对n∈N*恒成立,
∴k≥
对n∈N*恒成立,
令cn=
,cn-cn-1=
-
=
,当n≤3时,cn>cn-1,当n≥4时,cn<cn-1,
∴(cn)max=c3=
,
∴k≥
.
当n≥2时,4Sn-1=an2-4(n-1)-1,
∴4an=4Sn-4Sn-1=an+12-an2-4,
an+12=an2+4an+4=(an+2)2,
又an>0,∴an+1=an+2.
∴当n≥2时,{an}是公差d=2的等差数列.
又a2,a5,a14构成等比数列,a52=a2•a14,
(a2+6)2=a2•(a2+24),解得a2=3,
由条件可知,4a1=a22-5=4,∴a1=1,
又a2-a1=3-1=2,∴{an}是首项a1=1,公差d=2的等差数列.数列{an} 的通项公式为an=2n-1,
则b1=a2=3,b2=a5=9,b3=a14=27,且{bn}是等比数列,
∴数列{bn}的通项公式为bn=3n.
(Ⅱ)Tn=
| b1(1-qn) |
| 1-q |
| 3(1-3n) |
| 1-3 |
| 3n+1-3 |
| 2 |
∴(
| 3n+1-3 |
| 2 |
| 3 |
| 2 |
∴k≥
| 2n-4 |
| 3n |
令cn=
| 2n-4 |
| 3n |
| 2n-4 |
| 3n |
| 2n-6 |
| 3n-1 |
| -2(2n-7) |
| 3n |
∴(cn)max=c3=
| 2 |
| 27 |
∴k≥
| 2 |
| 27 |
点评:本题是对数列知识的考查,其中“迭代”思想是数列中最常见的思想,本题也不例外;在第二问的处理中,对于数列cn=
,通过作差研究数列的单调性也是与数列相关的综合性题型常用的方法.
| 2n-4 |
| 3n |

练习册系列答案
相关题目
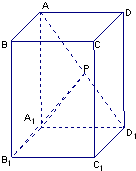 已知ABCD-A1B1C1D1是底面为正方形的长方体,∠AD1A1=60°,AD1=4,点P是AD1上的动点.
已知ABCD-A1B1C1D1是底面为正方形的长方体,∠AD1A1=60°,AD1=4,点P是AD1上的动点.