题目内容
已知函数f(x)=
,若f(x0)=2,则实数x0= ;函数f(x)的最大值为 .
|
考点:分段函数的应用
专题:计算题,函数的性质及应用
分析:利用分段函数,结合若f(x0)=2,可求实数x0;确定x≤0,x+3≤3;x>0,0<
<1,可得函数f(x)的最大值.
| 1 |
| x+1 |
解答:
解:x≤0,x+3=2,∴x=-1;x>0,
=2,x=-
(舍去);
x≤0,x+3≤3;x>0,0<
<1,∴函数f(x)的最大值为3.
故答案为:-1,3.
| 1 |
| x+1 |
| 1 |
| 2 |
x≤0,x+3≤3;x>0,0<
| 1 |
| x+1 |
故答案为:-1,3.
点评:本题考查分段函数的应用,考查函数的最值,考查学生的计算能力,比较基础.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
在极坐标系中,过点(2,
)且与极轴平行的直线方程是( )
| π |
| 2 |
| A、ρ=2 | ||
B、θ=
| ||
| C、ρcosθ=2 | ||
| D、ρsinθ=2 |
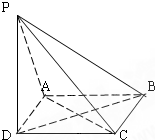 如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,PD=AD,
如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,PD=AD, 一个空间几何体的三视图如图所示,其中主视图和侧视图都是半径为1的圆,且这个几何体是实心球体的一部分,则这个几何体的体积为
一个空间几何体的三视图如图所示,其中主视图和侧视图都是半径为1的圆,且这个几何体是实心球体的一部分,则这个几何体的体积为