题目内容
在平面直角坐标系xOy中,点A,B的坐标分别为(-1,0),(1,0).设曲线C上任意一点P(x,y)满足|PA|=λ|PB|(λ>0且λ≠1).
(1)求曲线C的方程,并指出此曲线的形状;
(2)对λ的两个不同取值λ1,λ2,记对应的曲线为C1,C2.
(i)若曲线C1,C2关于某直线对称,求λ1,λ2的积;
(ii)若λ2>λ1>1,判断两曲线的位置关系,并说明理由.
(1)求曲线C的方程,并指出此曲线的形状;
(2)对λ的两个不同取值λ1,λ2,记对应的曲线为C1,C2.
(i)若曲线C1,C2关于某直线对称,求λ1,λ2的积;
(ii)若λ2>λ1>1,判断两曲线的位置关系,并说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由题意得
=λ
,由此能求出曲线C的方程,且曲线C是以(
,0)为圆心,
为半径的圆.
(2)(i)由(1)知曲线ci(i=1,2)是圆,当两圆关于某直线对称时,r1=r2,由此能求出λ1λ2=1.
(ii)由λ2>λ1>1,由已知条件推导出|O1O2|<|r2-r1|,从而得到圆O1与圆O2的位置关系是内含.
| (x+1)2+y2 |
| (x-1)2+y2 |
| λ2+1 |
| λ2-1 |
| 2λ |
| |λ2-1| |
(2)(i)由(1)知曲线ci(i=1,2)是圆,当两圆关于某直线对称时,r1=r2,由此能求出λ1λ2=1.
(ii)由λ2>λ1>1,由已知条件推导出|O1O2|<|r2-r1|,从而得到圆O1与圆O2的位置关系是内含.
解答:
解:(1)由题意得
=λ
,
两边平方并整理,得曲线C的方程为:
(λ2-1)x2+(λ2-1)y2-2(λ2+1)x+λ2-1=0,
∵λ>0,且λ≠1,∴曲线C的方程可化为:
(x-
)2+y2=(
)2,
∴曲线C是以(
,0)为圆心,
为半径的圆.
(2)(i)由(1)知曲线ci(i=1,2)是圆,
设圆心Oi(
,0),半径ri=
.
当两圆关于某直线对称时,r1=r2,
即
=-
,
∵λ1≠λ2,∴
=-
,
整理,得(λ1λ2-1)(λ1+λ2)=0,
∵λ1,λ2>0,∴λ1λ2=1.
(ii)∵λ2>λ1>1,
∴|O1O2|=|
-
|
=
=
,
|r2-r1|=|
-
|
=|
|
=
,
又∵(λ1+λ2)-(λ1λ2+1)=-(λ1-1)(λ2-1)<0,
∴|O1O2|<|r2-r1|,
∴圆O1与圆O2的位置关系是内含.
| (x+1)2+y2 |
| (x-1)2+y2 |
两边平方并整理,得曲线C的方程为:
(λ2-1)x2+(λ2-1)y2-2(λ2+1)x+λ2-1=0,
∵λ>0,且λ≠1,∴曲线C的方程可化为:
(x-
| λ2+1 |
| λ2-1 |
| 2λ |
| λ2-1 |
∴曲线C是以(
| λ2+1 |
| λ2-1 |
| 2λ |
| |λ2-1| |
(2)(i)由(1)知曲线ci(i=1,2)是圆,
设圆心Oi(
| λi2+1 |
| λi2-1 |
| 2λi |
| |λi2-1| |
当两圆关于某直线对称时,r1=r2,
即
| 2λ1 |
| |λ12-1| |
| 2λ2 |
| |λ22-1| |
∵λ1≠λ2,∴
| 2λ1 |
| λ12-1 |
| 2λ2 |
| λ22-1 |
整理,得(λ1λ2-1)(λ1+λ2)=0,
∵λ1,λ2>0,∴λ1λ2=1.
(ii)∵λ2>λ1>1,
∴|O1O2|=|
| λ12+1 |
| λ12-1 |
| λ22+1 |
| λ22-1 |
=
| 2(λ22-λ12) |
| (λ12-1)(λ22-1) |
=
| 2(λ2-λ1)(λ1+λ2) |
| (λ12-1)(λ22-1) |
|r2-r1|=|
| 2λ2 |
| λ22-1 |
| 2λ1 |
| λ12-1 |
=|
| 2(λ12-λ22λ1+λ1-λ2 |
| (λ12-1)(λ12-1) |
=
| 2(λ2-λ1)(λ1λ2+1) |
| (λ12-1)(λ22-1) |
又∵(λ1+λ2)-(λ1λ2+1)=-(λ1-1)(λ2-1)<0,
∴|O1O2|<|r2-r1|,
∴圆O1与圆O2的位置关系是内含.
点评:本题考查曲线方程的求法和曲线形状的判断,考查两实数积的求法,考查两圆位置关系的判断,解题时要认真审题,注意两点间距离公式的合理运用.

练习册系列答案
相关题目
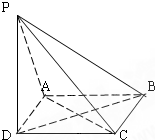 如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,PD=AD,
如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,PD=AD, 一个空间几何体的三视图如图所示,其中主视图和侧视图都是半径为1的圆,且这个几何体是实心球体的一部分,则这个几何体的体积为
一个空间几何体的三视图如图所示,其中主视图和侧视图都是半径为1的圆,且这个几何体是实心球体的一部分,则这个几何体的体积为