题目内容
设函数f(x)=|x-4|+|x-3|,
(Ⅰ)求f(x)的最小值m
(Ⅱ)当a+2b+3c=m(a,b,c∈R)时,求a2+b2+c2的最小值.
(Ⅰ)求f(x)的最小值m
(Ⅱ)当a+2b+3c=m(a,b,c∈R)时,求a2+b2+c2的最小值.
考点:二维形式的柯西不等式,绝对值不等式的解法
专题:选作题,不等式
分析:(Ⅰ)法1:f(x)=|x-4|+|x-3|≥|(x-4)-(x-3)|=1,可得函数f(x)的最小值;法2:写出分段函数f(x)=
,可得函数f(x)的最小值;
(Ⅱ)由柯西不等式(a2+b2+c2)(12+22+32)≥(a+2b+3c)2=1
|
(Ⅱ)由柯西不等式(a2+b2+c2)(12+22+32)≥(a+2b+3c)2=1
解答:
解:(Ⅰ)法1:f(x)=|x-4|+|x-3|≥|(x-4)-(x-3)|=1,
故函数f(x)的最小值为1.m=1.…(4分)
法2:f(x)=
.------------------(1分)
x≥4时,f(x)≥1;x<3时,f(x)>1,3≤x<4时,f(x)=1,----------------(3分)
故函数f(x)的最小值为1.m=1.…(4分)
(Ⅱ)由柯西不等式(a2+b2+c2)(12+22+32)≥(a+2b+3c)2=1----------(5分)
故a2+b2+c2≥
-…(6分)
当且仅当a=
,b=
,c=
时取等号…(7分)
故函数f(x)的最小值为1.m=1.…(4分)
法2:f(x)=
|
x≥4时,f(x)≥1;x<3时,f(x)>1,3≤x<4时,f(x)=1,----------------(3分)
故函数f(x)的最小值为1.m=1.…(4分)
(Ⅱ)由柯西不等式(a2+b2+c2)(12+22+32)≥(a+2b+3c)2=1----------(5分)
故a2+b2+c2≥
| 1 |
| 14 |
当且仅当a=
| 1 |
| 14 |
| 1 |
| 7 |
| 3 |
| 14 |
点评:本题考查绝对值不等式的解法,考查二维形式的柯西不等式,属于中档题.

练习册系列答案
相关题目
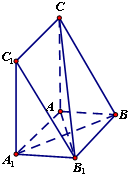 如图,三棱柱ABC-A1B1C1中,∠CAA1=∠A1AB=∠BAC=90°,AB=AA1=1,AC=2.
如图,三棱柱ABC-A1B1C1中,∠CAA1=∠A1AB=∠BAC=90°,AB=AA1=1,AC=2.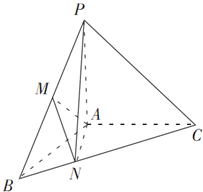 如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且AN=
如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且AN=