题目内容
8.从1,2,…,9这九个数中,随机抽取3个不同的数,则这3个数的和为奇数的概率是( )| A. | $\frac{5}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{11}{21}$ | D. | $\frac{10}{21}$ |
分析 先求出基本事件总数n=${C}_{9}^{3}$=84,再求出这3个数的和为奇数包含的基本事件个数m=${C}_{5}^{3}+{C}_{4}^{2}{C}_{5}^{1}$=40,由此能求出这3个数的和为奇数的概率.
解答 解:从1,2,…,9这九个数中,随机抽取3个不同的数,
基本事件总数n=${C}_{9}^{3}$=84,
这3个数的和为奇数包含的基本事件个数m=${C}_{5}^{3}+{C}_{4}^{2}{C}_{5}^{1}$=40,
∴这3个数的和为奇数的概率p=$\frac{m}{n}=\frac{40}{84}$=$\frac{10}{21}$.
故选:D.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
18.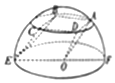 如图所示,三棱柱OAD-EBC,其中A,C,B,D,E均为以O为球心,半径为4的半球面上,EF为直径,侧面ABCD为边长等于4的正方形,则三棱柱OAD-EBC的高为( )
如图所示,三棱柱OAD-EBC,其中A,C,B,D,E均为以O为球心,半径为4的半球面上,EF为直径,侧面ABCD为边长等于4的正方形,则三棱柱OAD-EBC的高为( )
 如图所示,三棱柱OAD-EBC,其中A,C,B,D,E均为以O为球心,半径为4的半球面上,EF为直径,侧面ABCD为边长等于4的正方形,则三棱柱OAD-EBC的高为( )
如图所示,三棱柱OAD-EBC,其中A,C,B,D,E均为以O为球心,半径为4的半球面上,EF为直径,侧面ABCD为边长等于4的正方形,则三棱柱OAD-EBC的高为( )| A. | $\frac{8\sqrt{6}}{3}$ | B. | $\frac{4\sqrt{6}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
19.已知集合$P=\{x|y=\sqrt{2-x}\}$,Q={x|y=ln(x+1)},则P∩Q=( )
| A. | {x|-1≤x≤2} | B. | {x|-1≤x<2} | C. | {x|-1<x≤2} | D. | {x|-1<x<2} |
16.已知集合A={x|-1<x<2},B={x|0<x<3},则A∪B等于( )
| A. | (0,2) | B. | (2,3) | C. | (-1,3) | D. | (-1,0) |
20.用反证法证明命题“已知a、b、c为非零实数,且a+b+c>0,ab+bc+ca>0,求证a、b、c中至少有二个为正数”时,要做的假设是( )
| A. | a、b、c中至少有二个为负数 | B. | a、b、c中至多有一个为负数 | ||
| C. | a、b、c中至多有二个为正数 | D. | a、b、c中至多有二个为负数 |
17.倾斜角为120°且在y轴上的截距为-2的直线方程为( )
| A. | y=-$\sqrt{3}$x+2 | B. | y=-$\sqrt{3}$x-2 | C. | y=$\sqrt{3}$x+2 | D. | y=$\sqrt{3}$x-2 |
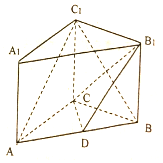 如图,已知在侧棱垂直于底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4点D是AB的中点.
如图,已知在侧棱垂直于底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4点D是AB的中点.