题目内容
18.若tan($α+\frac{π}{3}$)=2$\sqrt{3}$,则tan($α-\frac{2π}{3}$)的值是2$\sqrt{3}$,2sin2α-cos2α 的值是-$\frac{43}{52}$.分析 利用两角和差的正切公式、诱导公式求得tanα的值,再利用同角三角函数的基本关系求得要求式子的值.
解答 解:∵tan($α+\frac{π}{3}$)=2$\sqrt{3}$,
则tan($α-\frac{2π}{3}$)=tan[($α+\frac{π}{3}$)-π]=tan($α+\frac{π}{3}$)=2$\sqrt{3}$,
∵tan($α+\frac{π}{3}$)=$\frac{tanα+tan\frac{π}{3}}{1-tanα•tan\frac{π}{3}}$=$\frac{tanα+\sqrt{3}}{1-tanα•\sqrt{3}}$=2$\sqrt{3}$,∴tanα=$\frac{\sqrt{3}}{7}$,
∴2sin2α-cos2α=$\frac{{2sin}^{2}α{-cos}^{2}α}{{sin}^{2}α{+cos}^{2}α}$=$\frac{{2tan}^{2}α-1}{{tan}^{2}α+1}$=-$\frac{43}{52}$,
故答案为:$2\sqrt{3}$,$-\frac{43}{52}$;
点评 本题主要考查两角和差的正切公式、诱导公式、同角三角函数的基本关系的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.从1,2,…,9这九个数中,随机抽取3个不同的数,则这3个数的和为奇数的概率是( )
| A. | $\frac{5}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{11}{21}$ | D. | $\frac{10}{21}$ |
13.函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则ω,φ的值分别是( )

| A. | 2,-$\frac{π}{6}$ | B. | 2,-$\frac{π}{3}$ | C. | 4,-$\frac{π}{3}$ | D. | 4,-$\frac{π}{6}$ |
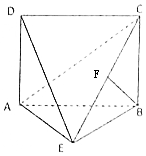 如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.
如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.