题目内容

17．倾斜角为120°且在y轴上的截距为-2的直线方程为（　　）
A．y=-$\sqrt{3}$x+2B．y=-$\sqrt{3}$x-2C．y=$\sqrt{3}$x+2D．y=$\sqrt{3}$x-2

分析 由直线的倾斜角求出斜率，然后直接由直线方程的斜截式得答案．

解答 解：∵tan120°=-$\sqrt{3}$，
∴所求直线的斜率为-$\sqrt{3}$，
又直线在y轴上的截距为-2，
由直线方程的斜截式得y=-$\sqrt{3}$x-2，
故选：B

点评 本题考查了直线的斜截式方程，考查了直线倾斜角与斜率的关系，是基础题．

练习册系列答案
相关题目
7．抛物线y=4x2的焦点到准线的距离为（　　）
A．2B．$\frac{1}{8}$C．4D．$\frac{1}{4}$
8．从1，2，…，9这九个数中，随机抽取3个不同的数，则这3个数的和为奇数的概率是（　　）
A．$\frac{5}{9}$B．$\frac{4}{9}$C．$\frac{11}{21}$D．$\frac{10}{21}$
5．l是经过双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）焦点F且与实轴垂直的直线，A，B是双曲线C的两个顶点，点在l存在一点P，使∠APB=60°，则双曲线离心率的最大值为$\frac{2\sqrt{3}}{3}$．
12．已知抛物线y2=2px（p＞0），F为其焦点，l为其准线，过F作一条直线交抛物线于A，B两点，A′，B′分别为A，B在l上的射线，M为A′B′的中点，给出下列命题：
①A′F⊥B′F；
②AM⊥BM；
③A′F∥BM；
④A′F与AM的交点在y轴上；
⑤AB′与A′B交于原点．
其中真命题的是①②③④⑤．（写出所有真命题的序号）
2．已知等边△ABC的边长为2$\sqrt{3}$，动点P、M满足|$\overrightarrow{AP}$|=1，$\overrightarrow{PM}$=$\overrightarrow{MC}$，则|$\overrightarrow{BM}$|2的最小值是（　　）
A．$\frac{25}{4}$B．$\frac{31}{4}$C．$\frac{37-6\sqrt{3}}{4}$D．$\frac{37-2\sqrt{33}}{4}$
9．已知圆C：（x-3）2+（y-4）2=4．
（Ⅰ） 若直线l过点A（2，3）且被圆C截得的弦长为2$\sqrt{3}$，求直线l的方程；
（Ⅱ） 若直线l过点B（1，0）与圆C相交于P，Q两点，求△CPQ的面积的最大值，并求此时直线l的方程．
6．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左焦点为F1（-1，0），P为椭圆上的顶点，且∠PF1O=45°（O为坐标原点）．
（1）求a，b的值；
（2）已知直线l1：y=kx+m1与椭圆交于A，B两点，直线l2：y=kx+m2（m1≠m2）与椭圆交于C，D两点，且|AB|=|CD|．
①求m1+m2的值；
②求四边形ABCD的面积S的最大值．
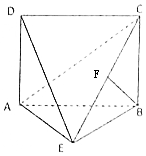7．如图，四边形ABCD为矩形，DA⊥平面ABE，AE=EB=BC=2，BF⊥平面ACE于点F，且点F在CE上．
（1）求证：AE⊥BE；
（2）求三棱锥C-ADE的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网