题目内容
3.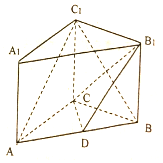 如图,已知在侧棱垂直于底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4点D是AB的中点.
如图,已知在侧棱垂直于底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4点D是AB的中点.(1)求证:AC1∥平面B1DC;
(2)求三棱锥A1-B1CD的体积.
分析 (1)设B1C∩BC1=E,连结DE,则DE∥AC1,由此能证明AC1∥平面B1DC.
(2)在△ABC中,过C作CF⊥AB,垂足为F,由${V}_{{A}_{1}-{B}_{1}CD}$=${V}_{C-{A}_{1}D{B}_{1}}$,能求出三棱锥A1-B1CD的体积.
解答 证明:(1)设B1C∩BC1=E,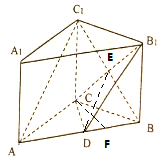
∵在侧棱垂直于底面的三棱柱ABC-A1B1C1中BB1C1C是矩形,∴E是BC1的中点,
连结DE,∵点D是AB的中点,∴DE∥AC1,
∵DE?平面B1DC,AC1?平面B1DC,
∴AC1∥平面B1DC.
解:(2)在△ABC中,过C作CF⊥AB,垂足为F,
由面ABB1A1⊥面ABC,知CF⊥面ABB1A1,
∴${V}_{{A}_{1}-{B}_{1}CD}$=${V}_{C-{A}_{1}D{B}_{1}}$,
∵${S}_{△D{A}_{1}{B}_{1}}$=$\frac{1}{2}{A}_{1}{B}_{1}•A{A}_{1}$=$\frac{1}{2}×5×4=10$,$CF=\frac{AC•BC}{AB}$=$\frac{3×4}{5}=\frac{12}{5}$.
三棱锥A1-B1CD的体积${V}_{{A}_{1}-{B}_{1}CD}$=${V}_{C-{A}_{1}D{B}_{1}}$=$\frac{1}{3}×10×\frac{12}{5}=8$.
点评 本题考查线面平行的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
13.已知f(x)=$\left\{\begin{array}{l}{e^x}+ax,x>0\\ \frac{1}{e^x}-ax,x<0\end{array}$,若函数f(x)有四个零点,则实数a的取值范围是( )
| A. | $({-∞,-\frac{1}{e}})$ | B. | (-∞,-e) | C. | (e,+∞) | D. | $({\frac{1}{e},+∞})$ |
18.拟定从甲地到乙地通话m分钟的电话费由f(m)=1.06(0.5•{m}+1)(元)决定,其中m>0,{m}是大于或等于m的最小整数,(如:{3}=3,{3.8}=4,{3.1}=4),则从甲地到乙地通话时间为5.5分钟的电话费为( )
| A. | 3.71元 | B. | 3.97元 | C. | 4.24元 | D. | 4.77元 |
8.从1,2,…,9这九个数中,随机抽取3个不同的数,则这3个数的和为奇数的概率是( )
| A. | $\frac{5}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{11}{21}$ | D. | $\frac{10}{21}$ |
13.函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则ω,φ的值分别是( )

| A. | 2,-$\frac{π}{6}$ | B. | 2,-$\frac{π}{3}$ | C. | 4,-$\frac{π}{3}$ | D. | 4,-$\frac{π}{6}$ |
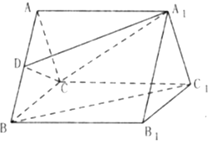 如图,在三棱柱ABC-A1B1C1中,侧棱垂直底面,各棱长均为2,D为AB的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直底面,各棱长均为2,D为AB的中点.