题目内容
12.已知函数f(x)=x3-3x2+2.(1)求函数的单调区间;
(2)求函数的极值.
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)求出函数的导数,解关于导函数的方程,求出函数的单调区间,从而求出函数的极值即可.
解答 解:(1)由f(x)=x3-3x2+2,所以f′(x)=3x2-6x=3x(x-2).…(2分)
由f′(x)>0知:x<0或x>2时;由f′(x)<0知:0<x<2时. …(5分)
所以,函数f(x)的单调递增区间是(-∞,0),(2,+∞).单调递减区间是(0,2). …(6分)
(2)f′(x)=3x2-6x.令f′(x)=0,解得x=2或x=0,…(7分)
当x变化时,f′(x),f(x)的变化情况如下表:…(10分)
| x | (-∞,0) | 0 | (0,1) | 2 | (1,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | ↑ | 2 | ↓ | -2 | ↑ |
当x=0时,f(x)有极大值,且f(0)=2…(12分)
点评 本题考查了函数的单调性、极值问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
4.定义在R上的奇函数f(x)满足f(x)=-f(x+2),且在[1,2]上是减函数,则( )
| A. | $f(\frac{1}{2})<f(-\frac{3}{2})<f(3)$ | B. | $f(3)<f(-\frac{3}{2})<f(\frac{1}{2})$ | C. | $f(\frac{1}{2})<f(3)<f(-\frac{3}{2})$ | D. | $f(3)<f(\frac{1}{2})<f(-\frac{3}{2})$ |
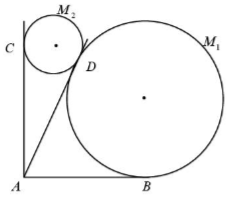 某景区欲建两条圆形观景步道M1,M2(宽度忽略不计),如图所示,已知AB⊥AC,AB=AC=AD=60(单位:米),要求圆M与AB,AD分别相切于点B,D,圆M2与AC,AD分别相切于点C,D.
某景区欲建两条圆形观景步道M1,M2(宽度忽略不计),如图所示,已知AB⊥AC,AB=AC=AD=60(单位:米),要求圆M与AB,AD分别相切于点B,D,圆M2与AC,AD分别相切于点C,D.