题目内容
7.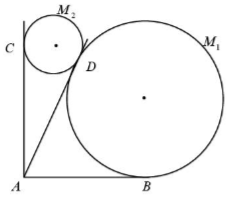 某景区欲建两条圆形观景步道M1,M2(宽度忽略不计),如图所示,已知AB⊥AC,AB=AC=AD=60(单位:米),要求圆M与AB,AD分别相切于点B,D,圆M2与AC,AD分别相切于点C,D.
某景区欲建两条圆形观景步道M1,M2(宽度忽略不计),如图所示,已知AB⊥AC,AB=AC=AD=60(单位:米),要求圆M与AB,AD分别相切于点B,D,圆M2与AC,AD分别相切于点C,D.(1)若$∠BAD=\frac{π}{3}$,求圆M1,M2的半径(结果精确到0.1米)
(2)若观景步道M1,M2的造价分别为每米0.8千元与每米0.9千元,则当∠BAD多大时,总造价最低?最低总造价是多少?(结果分别精确到0.1°和0.1千元)
分析 (1)利用切线的性质即可得出圆的半径;
(2)设∠BAD=2α,则总造价y=0.8•2π•60tanα+0.9•2π•60tan(45°-α),化简,令1+tanα=x换元,利用基本不等式得出最值.
解答 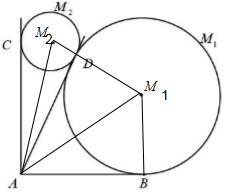 解:(1)连结M1M2,AM1,AM2,
解:(1)连结M1M2,AM1,AM2,
∵圆M1与AB,AD相切于B,D,圆M2与AC,AD分别相切于点C,D,
∴M1,M2⊥AD,∠M1AD=$\frac{1}{2}$∠BAD=$\frac{π}{6}$,∠M2AD=$\frac{π}{12}$,
∴M1B=ABtan∠M1AB=60×$\frac{\sqrt{3}}{3}$=20$\sqrt{3}$≈34.6(米),
∵tan$\frac{π}{6}$=$\frac{2tan\frac{π}{12}}{1-ta{n}^{2}\frac{π}{12}}$=$\frac{\sqrt{3}}{3}$,∴tan$\frac{π}{12}$=2-$\sqrt{3}$,
同理可得:M2D=60×tan$\frac{π}{12}$=60(2-$\sqrt{3}$)≈16.1(米).
(2)设∠BAD=2α(0<α<$\frac{π}{4}$),由(1)可知圆M1的半径为60tanα,圆M2的半径为60tan(45°-α),
设观景步道总造价为y千元,则y=0.8•2π•60tanα+0.9•2π•60tan(45°-α)=96πtanα+108π•$\frac{1-tanα}{1+tanα}$,
设1+tanα=x,则tanα=x-1,且1<x<2.
∴y=96π(x-1)+108π($\frac{2}{x}-1$)=12π•(8x+$\frac{18}{x}$-17)≥84π≈263.8,
当且仅当8x=$\frac{18}{x}$即x=$\frac{3}{2}$时取等号,
当x=$\frac{3}{2}$时,tanα=$\frac{1}{2}$,∴α≈26.6°,2α≈53.2°.
∴当∠BAD为53.2°时,观景步道造价最低,最低造价为263.8千元.
点评 本题考查直线与圆的位置关系,考查基本不等式的运用,属于中档题.

 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案| A. | 25 | B. | 49 | C. | 15 | D. | 40 |
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}或\frac{2π}{3}$ |
| 男 | 女 | 总计 | |
| 爱好 | 10 | 40 | 50 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 30 | 70 | 100 |
| A. | 0.25% | B. | 2.5% | C. | 97.5% | D. | 99.75% |