题目内容
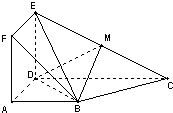 如图多面体中,正方形ADEF所在的平面与直角梯形ABCD所在的平面垂直,且AD=AB=
如图多面体中,正方形ADEF所在的平面与直角梯形ABCD所在的平面垂直,且AD=AB=| 1 |
| 2 |
(1)证明:BM∥平面ADEF;
(2)证明:平面BCE⊥平面BDE.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(1)取DE中点N,连接MN,AN,由三角形中位线定理,结合已知中AB∥CD,AB=AD=2,CD=4,易得四边形ABMN为平行四边形,所以BM∥AN,再由线面平面的判定定理,可得BM∥平面ADEF;
(2)由已知中正方形ADEF与梯形ABCD所在的平面互相垂直,易得ED⊥平面ABCD,进而ED⊥BC,由勾股定理,我们易判断出△BCD中,BC⊥BD,由线面垂直的判定定理可得BC⊥平面BDE,再由面面垂直的判定定理,即可得到平面BCE⊥平面BDE.
(2)由已知中正方形ADEF与梯形ABCD所在的平面互相垂直,易得ED⊥平面ABCD,进而ED⊥BC,由勾股定理,我们易判断出△BCD中,BC⊥BD,由线面垂直的判定定理可得BC⊥平面BDE,再由面面垂直的判定定理,即可得到平面BCE⊥平面BDE.
解答:
 证明:(1)取DE中点N,连接MN,AN
证明:(1)取DE中点N,连接MN,AN
在△EDC中,M、N分别为EC,ED的中点,所以MN∥CD,且MN=
CD.
由已知AB∥CD,AB=
CD,所以MN∥AB,且MN=AB.
所以四边形ABMN为平行四边形,所以BM∥AN
又因为AN?平面ADEF,
且BM?平面ADEF,
所以BM∥平面ADEF.
(2)在正方形ADEF中,ED⊥AD,
又因为平面ADEF⊥平面ABCD,
且平面ADEF∩平面ABCD=AD,
所以ED⊥平面ABCD,所以ED⊥BC.
在直角梯形ABCD中,
AB=AD=2,CD=4,可得BC=2
在△BCD中,BD=BC=2
,CD=4,
所以BC⊥BD.
所以BC⊥平面BDE,
又因为BC?平面BCE,
所以平面BCE⊥平面BDE.
 证明:(1)取DE中点N,连接MN,AN
证明:(1)取DE中点N,连接MN,AN在△EDC中,M、N分别为EC,ED的中点,所以MN∥CD,且MN=
| 1 |
| 2 |
由已知AB∥CD,AB=
| 1 |
| 2 |
所以四边形ABMN为平行四边形,所以BM∥AN
又因为AN?平面ADEF,
且BM?平面ADEF,
所以BM∥平面ADEF.
(2)在正方形ADEF中,ED⊥AD,
又因为平面ADEF⊥平面ABCD,
且平面ADEF∩平面ABCD=AD,
所以ED⊥平面ABCD,所以ED⊥BC.
在直角梯形ABCD中,
AB=AD=2,CD=4,可得BC=2
| 2 |
在△BCD中,BD=BC=2
| 2 |
所以BC⊥BD.
所以BC⊥平面BDE,
又因为BC?平面BCE,
所以平面BCE⊥平面BDE.
点评:本题考查的知识点是直线与平面平行的判定,平面与平面垂直的判定,熟练掌握空间直线与平面不同位置关系(平行和垂直)的判定定理、性质定理、定义及几何特征是解答本题的关键.

练习册系列答案
相关题目
在△ABC中,角A,B,C所对的边分别为a,b,c,则下列判断中正确的是( )
| A、a=30,b=25,A=150°,有一解 |
| B、a=7,b=14,A=30°,有两解 |
| C、a=6,b=9,A=45°,有两解 |
| D、b=9,c=10,B=60°,无解 |
 给定椭圆C:
给定椭圆C: 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<