题目内容
O为△ABC所在平面内的一点，若
+
+
=
，则O必是△ABC的 ．（填写“内心”、“重心”、“垂心”、“外心”之一）
| OA |
| OB |
| OC |
| 0 |
考点：三角形五心
专题：计算题,平面向量及应用
分析：取BC中点D，连接并延长OD至E，使DE=OD 于是四边形BOCE是平行四边形，由条件和共线向量定理，即可得到AD为中线，同理延长BO交AC于F，则F也为中点，即可得到O是重心．
解答：
解：取BC中点D，连接并延长OD至E，使DE=OD 于是四边形BOCE是平行四边形，
∵
+
=
，又
+
+
=
，∴
=
=2
，
∴A，O，D，E四点共线，即AD是中线，
同理延长BO交AC于F，则F也为中点，
∴O是重心．
故答案为：重心
解：取BC中点D，连接并延长OD至E，使DE=OD 于是四边形BOCE是平行四边形，∵
| OB |
| OC |
| OE |
| OA |
| OB |
| OC |
| 0 |
| AO |
| OE |
| OD |
∴A，O，D，E四点共线，即AD是中线，
同理延长BO交AC于F，则F也为中点，
∴O是重心．
故答案为：重心
点评：本题考查平面向量的运用，考查向量加法的平行四边形法则，同时考查三角形的重心定义，属于中档题．
练习册系列答案
相关题目
设函数f（x）=
，若f（a）=1，则实数a的值为（ ）
|
| A、-1或0 | B、2或-1 |
| C、0或2 | D、2 |
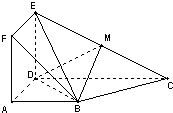如图多面体中，正方形ADEF所在的平面与直角梯形ABCD所在的平面垂直，且AD=AB=