题目内容
已知双曲线C1:
-8y2=1(a>0)的离心率是
,抛物线C2:y2=2px的准线过C1的左焦点.
(1)求抛物线C2的方程;
(2)若A(x1,y1),B(x2,y2),C(x3,4)是C2上三点,且CA⊥CB,证明:直线AB过定点,并求出这个定点的坐标.
| x2 |
| a2 |
| 2 |
(1)求抛物线C2的方程;
(2)若A(x1,y1),B(x2,y2),C(x3,4)是C2上三点,且CA⊥CB,证明:直线AB过定点,并求出这个定点的坐标.
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)双曲线C1:
-8y2=1(a>0)的离心率是
,所以a2=
,c2=
,即可求抛物线C2的方程;
(2)求出A,B的坐标,可得直线AB的方程,即可得出结论.
| x2 |
| a2 |
| 2 |
| 1 |
| 8 |
| 1 |
| 4 |
(2)求出A,B的坐标,可得直线AB的方程,即可得出结论.
解答:
解:(1)因为双曲线C1:
-8y2=1(a>0)的离心率是
,
所以a2=
,c2=
,…(2分)
所以抛物线C2:y2=2px的准线方程是x=-
,
所以p=1,抛物线C2的方程是y2=2x. …(4分)
(2)不妨设C(8,4),
设AC的斜率为k,则直线AC的方程是y-4=k(x-8),
x=
代入并整理,得ky2-2y+8-8k=0,
方程的两根是4和
-4,所以y1=
-4,x1=
,
A点的坐标是(
,
-4),
同理可得B点的坐标(2(2+k)2,-2k-4),…(7分)
直线AB的斜率kAB=
,
直线AB的方程是y-(-2k-4)=
[x-2(2+k)2],
即y=
(x-10)-4,…(9分)
直线AB过定点,定点坐标是(10,-4). …(10分)
| x2 |
| a2 |
| 2 |
所以a2=
| 1 |
| 8 |
| 1 |
| 4 |
所以抛物线C2:y2=2px的准线方程是x=-
| 1 |
| 2 |
所以p=1,抛物线C2的方程是y2=2x. …(4分)
(2)不妨设C(8,4),
设AC的斜率为k,则直线AC的方程是y-4=k(x-8),
x=
| y2 |
| 2 |
方程的两根是4和
| 2 |
| k |
| 2 |
| k |
| 2(2k-1)2 |
| k2 |
A点的坐标是(
| 2(2k-1)2 |
| k2 |
| 2 |
| k |
同理可得B点的坐标(2(2+k)2,-2k-4),…(7分)
直线AB的斜率kAB=
| -k |
| k2+4k-1 |
直线AB的方程是y-(-2k-4)=
| -k |
| k2+4k-1 |
即y=
| -k |
| k2+4k-1 |
直线AB过定点,定点坐标是(10,-4). …(10分)
点评:本题主要考查了直线与曲线方程的位置关系及方程思想的转化,方程的根与系数的关系的应用,抛物线的定义的应用.综合的知识的较多,还有具备一定的计算及推理的能力.

练习册系列答案
相关题目
已知定义域为R的函数f(x)满足f(2+x)=f(2-x)对任意实数x恒成立,当x≥2时,f(x)为增函数,则下列关系一定正确的是( )
| A、f(7)<f(-2) |
| B、f(7)>f(-2) |
| C、f(6)>f(-2) |
| D、f(6)<f(-2) |
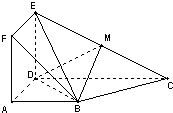 如图多面体中,正方形ADEF所在的平面与直角梯形ABCD所在的平面垂直,且AD=AB=
如图多面体中,正方形ADEF所在的平面与直角梯形ABCD所在的平面垂直,且AD=AB=