题目内容
证明：
-
=
．
| 1 |
| 2x2 |
| 1 |
| 2x1 |
| 2x1-2x2 |
| 2x1+x2 |
考点：综合法与分析法(选修）
专题：推理和证明
分析：将所证的关系式的左端通分后整理即可证得结论成立．
解答：
证明：∵
-
=
=
．
∴原结论成立．
| 1 |
| 2x2 |
| 1 |
| 2x1 |
| 2x1-2x2 |
| 2x1•2x2 |
| 2x1-2x2 |
| 2x1+x2 |
∴原结论成立．
点评：本题考查综合法证明恒等式，考查指数函数的运算性质的应用，属于中档题．
练习册系列答案
同步练习强化拓展系列答案
相关题目
已知y=f（x）为定义在R上的函数，则“存在X0∈R，使得f2（-x0）≠f2（x0）”是“f（x）为非奇非偶函数”的（ ）
| A、充分非必要 |
| B、必要非充分 |
| C、充分必要 |
| D、既不充分也不必要 |
已知定义域为R的函数f（x）满足f（2+x）=f（2-x）对任意实数x恒成立，当x≥2时，f（x）为增函数，则下列关系一定正确的是（ ）
| A、f（7）＜f（-2） |
| B、f（7）＞f（-2） |
| C、f（6）＞f（-2） |
| D、f（6）＜f（-2） |
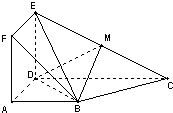如图多面体中，正方形ADEF所在的平面与直角梯形ABCD所在的平面垂直，且AD=AB=